Преждевременная оптимизация
Пригорело от очередного рассуждения в интернетиках о том, что цитата Кнута про “корень всех зол” она вовсе не про оптимизации и не про эффективный код, а “всего лишь про использование операторов go to”. Ну, думаю, сейчас покажу, что там Кнут на самом деле имел в виду… Но оказалось, что внятно сослаться-то и не на что. Нет ни переводов, ни какого-то разбора, сделанного в конце 20 века или позже, а просто так на оригинал и не сошлёшься: один-в-один занудный трёхтомник, за прочтение которого Гейтс обещал трудоустройство в Microsoft.
Поэтому собрал собственное. Близко к оригиналу, но всё-таки не оригинал. Некоторые детали, а также моменты, острые в 1974 году, но малоизвестные сейчас, как, например, идеи “Новой Математики” и т.п., опущены, если не получалось кратко пояснить, о чём идёт речь и почему это важно.
И, да, это статья не про операторы go to. Это статья о написании эффективных программ, а go to - это чуть ли не единственный инструмент, доступный программистам шестидесятых для проведения оптимизаций на языках высокого уровня.
Важные моменты: Передовым языком в 1974 году был ALGOL, поэтому рассуждения по тексту статьи относятся, в основном, к нему. И надо понимать, как в то время писали программы. К написанию реального кода не приступали, не собрав предварительно требования и не нарисовав блок-схему, и не реализовав планируемый алгоритм на псевдокоде, что-то типа этого:
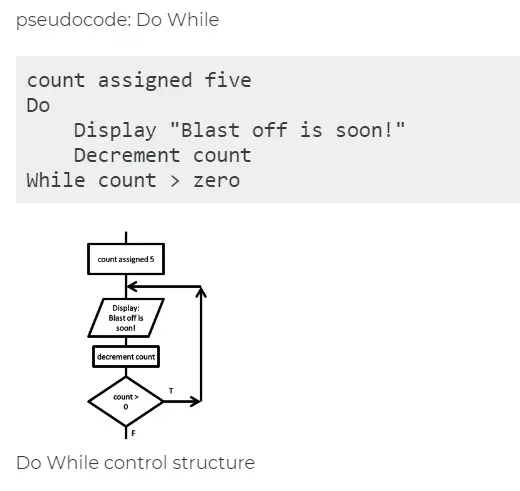
Терпеливым занудам же рекомендую первоисточник: D. Knuth. “Structured Programming with go to Statements”
1974, Дональд Кнут, “Структурное программирование с операторами go to”
Рассмотрим несколько примеров, проливающих свет на проблему создания надёжных, хорошо структурированных и эффективных программ. Исследование будет посвящено двум вопросам:
- новому синтаксису для написания циклов и выходов при ошибке, что позволит писать программы ясно и эффективно без операторов
go to; - методологии проектирования, начинающейся с понятных и корректных, но, возможно, неэффективных программ, которые, при необходимости, системно преобразуются в более эффективный, но, возможно, менее читаемый код.
Будут высказаны противоположные точки зрения на необходимость отмены операторов go to. И будет сделана попытка определить истинную природу структурного программирования, и даны рекомендации для дальнейшего изучения.
Введение
В сфере написания программ и преподавания программирования происходит революция, поскольку мы начинаем глубже понимать связанные с ними ментальные процессы. Невозможно прочитать книгу “Структурное программирование” (Даль, Дейкстра, Хоар, 1972), и жить прежней жизнью. Причины этой революции и её перспективы ярко описаны Дейкстрой в его лекции 1972 года “Скромный программист”, за которую он получил премию Тьюринга.
По мере роста нашего опыта, каждый из нас развивает свои убеждения в ту или иную сторону, соглашаясь или не соглашаясь с лидерами этой революции. Должен признать, что я являюсь нескромным программистом, причём эгоистичным настолько, что я верю, что моё собственное мнение о текущих тенденциях не является пустой тратой времени читателя. Поэтому я хочу поделиться в этой статье некоторыми фактами, которые поразили меня наиболее сильно во время размышлений о структурном программировании в течение последнего года. Почти все идеи, которые я буду обсуждать, не являются моими собственными, но, возможно, я представлю их в новом свете. Я пишу эту статью от первого лица, чтобы подчеркнуть, что я выражаю лишь собственное мнение. И я не надеюсь убедить всех в том, что мои сегодняшние взгляды верны.
Прежде чем начать обсуждение сугубо технических деталей, я должен признаться, что название этой статьи специально выбрано таким для привлечения внимания. Безусловно, некоторые читатели убеждены, что отмена операторов go to - всего лишь модная причуда, и, увидев это название, они могут подумать: “Ага! Кнут реабилитирует go to, мы можем вернуться к нашим старым методам программирования.” Другая группа читателей, увидев это еретическое название, подумает: “Когда уже такие консерваторы, как Кнут, смирятся с реальностью?” Я надеюсь, что обе группы людей продолжат чтение и обнаружат, что на самом деле я стремлюсь к достижению разумно сбалансированной точки зрения относительно роли операторов go to. Я выступаю за удаление операторов go to в некоторых случаях и за их добавление в других.
Излагая такую точку зрения, я на самом деле довольно близок к идеям Дейкстры, который недавно написал следующее: “Пожалуйста, не попадайте в ловушку, считая, что я ужасно догматичен по отношению к [оператору go to]. У меня есть неприятное ощущение, что некоторые строят из этого религию, как будто концептуальные проблемы программирования могут быть решены одним махом, только лишь простой сменой формы написания кода!”
Другими словами, кажется, что фанатичные сторонники “Нового Программирования” перегибают палку в своём строгом соблюдении чистоты в программах. Рано или поздно люди обнаружат, что их прекрасно структурированные программы работают всего лишь в половину скорости старых грязных программ, которые они писали раньше, и они, конечно, обвинят в этом структурный подход, вместо того чтобы признать, что настоящая причина - накладные расходы, которые возникают в коде, сгенерированном типичным компилятором: методы обращения с переменными и вызовы процедур. И тогда у нас произойдёт прискорбная контрреволюция, что-то вроде сегодняшнего отказа от “Новой Математики” в ответ на её слишком уж насильственные реформы.
В конце 1960-х годов мы стали свидетелями кризиса программного обеспечения, который многим показался парадоксальным, ведь ожидалось, что программировать - это просто. В результате люди начали отказываться от тех возможностей, которые, теоретически, способны привести к усложнению кода. И вопросы возникли не только к операторам go to. Также растёт недовольство вычислениями с плавающей точкой, глобальными переменными, семафорами, указателями и даже операторами присваивания. Скоро, видимо, докатимся до десятка простых одобренных программ, использование которых будет считаться приемлемым. Вот тогда программы точно не причинят нам проблем. Правда, и применить их будет почти негде.
Я думаю, что мы сейчас наконец-то близки к открытию того, какими на самом деле должны быть языки программирования, и с нетерпением жду результатов множества экспериментов над дизайном языков. И мечтаю о том, что к 1984 году наши споры приведут к созданию действительно хорошего языка программирования (или семейства). Более того, я предполагаю, что люди настолько разочаруются в используемых сейчас COBOL и FORTRAN, что этот новый UTOPIA 84, получит шанс. До этого ещё далеко, конечно, но признаки формирования этого нового языка уже видны.
Будут ли в UTOPIA 84 (или, может, в NEWSPEAK?) операторы go to? На сегодня, к сожалению, нет единого мнения по этому, казалось бы, пустяковому вопросу. И нам лучше не застревать на нём слишком долго, ведь до 84 года осталось всего десять лет.
Я постараюсь подробно разобрать спор о go to, рассматривая аргументы как за, так и против, и не занимая твёрдой позиции той или иной стороны. Чтобы проиллюстрировать различные варианты использования операторов go to, я рассмотрю множество примеров, притом, выводы из разбора одних будут противоречить выводам из других.
Есть две причины, по которым я решил изложить материал в такой, на первый взгляд, странной манере. Во-первых, поскольку у меня есть возможность выбирать любые примеры, я не считаю справедливым выбирать только те фрагменты программ, которые выгораживают лишь одну сторону спора. Во-вторых, и это, пожалуй, самое важное, я опробовал этот подход, когда читал лекцию в Калифорнийском университете в феврале 1974 года, и он прекрасно сработал: почти у каждого в аудитории сложилась иллюзия, что я в значительной степени поддерживаю его взгляды, какими бы эти взгляды не были!
1. Удаление операторов go to
Историческая справка
На конгрессе IFIP в 1971 году я имел удовольствие познакомиться с доктором Эйити Гото из Японии, который весело жаловался, что его постоянно удаляют. Это была вся история, насколько мне удалось её изучить.
Одним из первых программистов, которые систематически начали избегать применения меток и операторов go to, был Шорре из Калифорнийского университета в Лос-Анджелесе. О своих ранних опытах он писал:
С лета 1960 года я пишу черновики программ, используя отступы для обозначения потока управления. Мне никогда не приходилось нарушать мою систему отступов и использовать оператор go to. Я сохранял эти черновики в качестве документации к программе, вместо использования традиционных блок-схем. Затем я писал программу на языке ассемблера, руководствуясь этим документом. Мой подход всем нравится больше, чем блок-схемы, которые я рисовал раньше, и которые у меня получались не очень симпатичными - их обзывали “шар-о-граммами”.
По его мнению этот подход упрощает разработку программ, их чтение и сопровождение.
Когда я познакомился с Шорре в 1963 году и он рассказал о своих радикальных идеях, я сходу не поверил, что они работают. Честно говоря, я думал, что он просто оправдывается за то, что не смог добавить метки и операторы go to в свой язык META-II, который мне очень нравился, за исключением этого упущения. В 1964 году я попросил его написать программу для задачи о восьми ферзях без использования операторов go to, и он выдал текст с рекурсивными процедурами и булевыми флагами, очень похожий на программу, позже независимо опубликованную Виртом.
Я не был уверен, что от всех операторов go to можно или нужно отказываться, но полностью поддерживал Питера Наура, опубликовавшем в 1963 первые замечания:
Если вы обратите внимание, то обнаружите, что удивительно часто оператор go to, который выполняет переход назад, это на самом деле просто неявный оператор for. И вы будете приятно удивлены, как улучшится ясность алгоритма, когда вы напишете оператор for там, где он и должен быть… Если целью [курса программирования] является обучение программированию на ALGOL, то использование при этом блок-схем, на мой взгляд, приносит больше вреда, чем пользы.
А в 1965 году к нему присоединился Эдсгер Дейкстра:
Два менеджера отделов программирования из разных стран и разных направлений - один в основном научного, другой - коммерческого, независимо друг от друга и по собственной инициативе сообщили мне о своем наблюдении, что качество их программистов обратно пропорционально плотности операторов go to в их программах… Я проводил различные эксперименты в области программирования… в модифицированных версиях ALGOL 60, из которых операторы go to были удалены… Последние версии создавать было сложно: мы так привыкли к команде перехода, что требуется некоторое усилие, чтобы её забыть! Однако во всех случаях программа без операторов go to оказывалась короче и понятнее.
Несколько месяцев спустя, на конференции ACM Programming Languages and Pragmatics Conference, высказался и Питер Лэндин:
Есть такая игра, в которую иногда играют на ALGOL 60 - переписывание программ так, чтобы не использовать операторы go to. Это часть другой большой игры - уменьшения сложности программы, путём сокращения степени её ветвления… Важность этой игры заключается в том, что она часто приводит к более “прозрачным” программам - их легче понять, отладить, модифицировать и интегрировать в крупные системы.
Следующую главу в этой истории многие считают первой, потому что она вызвала наибольший резонанс. Дейкстра в 1968 году отправил в Communications of the ACM небольшую статью, полностью посвященную обсуждению операторов go to. А чтобы ускорить публикацию, и подогреть интерес, редактор решил опубликовать статью Дейкстры в виде письма и снабдить её новым заголовком: “Операторы go to считаются вредными”.
Эта заметка быстро стала известной. Она выражала убеждение Дейкстры в том, что “операторы go to нужно убрать из вообще всех языков программирования высокого уровня… Оператор go to в его нынешнем виде просто слишком примитивен: он провоцирует на создание беспорядка в программе” и призывала искать альтернативные конструкции. Дейкстра упоминал, что не только Хайнц Земанек выражал сомнения по поводу операторов go to еще в 1959 году, но определенное влияние оказали Питер Лэндин, Кристофер Стрейчи, Хоар и другие.
К 1967 году Маккиман, Хорнинг и Вортман написали компилятор XPL, использовав оператор go to только единожды. В 1971 году Кристофер Стрейчи заявил: “Моя цель - писать программы без меток. И у меня это неплохо получается. Я уменьшил количество меток в операционной системе до 5 и планирую написать компилятор вообще без меток”. В 1972 году этой теме была посвящена целая сессия Национальной конференции ACM. В декабрьском номере журнала Datamation за 1973 год было опубликовано пять статей о структурном программировании и устранении go to.
Очевидно, что настроения против оператора go to росли. Также рос и накал споров. Дейкстра однажды признался мне, что после публикации своей статьи он получил “вал оскорбительных писем”.
Меня новое веяние впервые коснулось в 1969 году, когда я начал преподавать вводный курс программирования. Помню, как я не понимал, как писать программы в новом стиле и в бессилии бегал в офис Боба Флойда за помощью, и он обычно показывал мне, что нужно делать. Так родилась наша статья, в которой мы представили два типа программ, из которых не удавалось убрать go to. Мы обнаружили, что не существует способа реализовать некоторые простые конструкции с помощью условных операторов и while, если не прибегать к дополнительным вычислениям.
В последние несколько лет появились языки, разработчики которых с гордостью объявили, что избавились от оператора go to. Пожалуй, самым известным из них является Bliss, который заменил операторы go to на восемь так называемых “операторов выхода”. И даже восьми было недостаточно. Авторы писали: “Мы ошиблись в предположении, что раз мы удалили оператор go to, то и метки больше не нужны”, и позже добавили новое выражение “leave <label> with <expression>”, которое передаёт управление следующему оператору после обозначенного <label>. В других языках системного программирования, также избавившихся от go to, сходным образом появились операторы, которые предоставляют “столь же мощные” альтернативные способы передачи управления.
Другими словами, кажется, что все согласны с тем, что операторы go to - это плохо, но программисты и разработчики языков программирования всё равно нуждаются в каком-то эвфемизме, который бы выполнял “переход к” некоторому фрагменту программы, но не назывался бы go to.
На примере поиска
Зачем это всё? В “Notes on avoiding 'go to' statements” мы с Флойдом привели пример типичной программы, для которой возможностей операторов while и if недостаточно. Предположим, что мы хотим выполнить поиск в таблице различных значений A[1] ... A[m] и найти, где встречается некоторое значение x. Если x не присутствует в таблице, то вставить его в качестве новой записи. Предположим также, что существует еще один массив B, в котором B[i] равно количеству раз, когда мы искали значение A[i].
Можно решить такую задачу следующим образом:
Пример 1:
for i := 1 step 1 until m do
if A[i] = x then go to found fi;
not found: i := m+1; m := i;
A[i] := x; B[i] := 0;
found: B[i] := B[i]+1;
В этой статье я буду использовать искусственный язык программирования, похожий на ALGOL 60, за одним исключением: символ fi используется в качестве закрывающей последовательности для выражений if, так что между then и else не будут нужны begin и end. Мне не очень нравится, как выглядит fi, но он короткий, полезный и работает, так что я надеюсь, что привыкну.
Есть способы написать пример 1 без оператора go to, но они потребуют больше вычислений и будут хуже читаться. Этот пример широко цитируется защитниками оператора, и поэтому к этой задаче нужно подойти более ответственно.
Допустим, что нам запретили использовать операторы go to, а мы хотим выполнить именно те вычисления, которые указаны в примере 1 (используя очевидную замену оператора for на присваивание и while). Если же мы хотим не просто получить те же результаты, но и выполнять те же операции в том же порядке, то задание невыполнимо.
Но если немного ослабить требования и проверять условие дважды подряд (если у него нет побочных эффектов), то задачу можно решить следующим образом:
Пример 1a:
i := 1;
while i <= m and A[i] != x do i := i+1;
if i > m then m := i; A[i] := x; B[i] := 0 fi;
B[i] := B[i]+1;
Используемая здесь операция and означает оператор последовательной конъюнкции Маккарти, т. е. “p and q” означает “if p then q else false fi”, так что q не вычисляется, если p ложно. В примере 1a выполняется точно такая же последовательность вычислений, как и в примере 1, за исключением одного дополнительного сравнения i с m (и иногда на одно вычисление m + 1 меньше). Если итерации в цикле while выполняются много раз, то дополнительное сравнение влияет на общее время работы незначительно.
Таким образом, мы можем избавиться от go to в примере 1. Но пример 1a, на мой взгляд, чуть менее читабелен, а также чуть медленнее, так что не совсем понятно, что мы тут выиграли. Более того, если бы мы усложнили пример 1, то трюк с переходом к примеру 1a уже не сработал бы. Например, предположим, что мы вставили в цикл for ещё одно выражение, непосредственно перед условием if. Тогда сравнения i <= m и A[i] = x не стояли бы рядом, и мы не смогли бы, в общем случае, объединить их с помощью and.
Джон Кок рассказал мне поучительную историю, связанную с примером 1 и с проектированием языков. Некоторых программистов на PL/I попросили решить поставленную задачу поиска без использования go to, и они предложили следующие два варианта:
а)
DO I = 1 to M WHILE A(I) != X;
END;
IF I > M THEN
DO; M = I; A(I) = X; B(I) = 0; END;
B(I) = B(I) + 1;
б)
FOUND = 0
DO I = 1 TO M WHILE FOUND = 0;
IF A(I) = X THEN FOUND = 1;
END;
IF FOUND = 0 THEN
DO; M = I; A(I) = X; B(I) = 0; END;
B(I) = B(I) + 1;
Решение (а) лучше, но поскольку в нём есть цикл с пустым телом, большинству людей нравится решение (б).
Поучительно, что решение (б) не работает. В нём допущена серьёзная ошибка. Дело в том, что переменная I увеличивается до того, как проверяется значение FOUND. Один из способов исправить программу - вставить I = I - FOUND; перед последним оператором.
Как я уже говорил, пример 1 часто используется для защиты оператора go to. Однако, к сожалению, этот пример совершенно неубедителен, несмотря на приведённые мною аргументы, потому что алгоритм из примера 1 почти никогда не является хорошим способом поиска в массиве! Следующая модификация значительно улучшает алгоритм:
Пример 2:
A[m+1] := x; i := 1;
while A[i] != x: do i := i+1;
if i > m then m := i; B[i] := 1;
else B[i] := B[i]+1 fi;
Пример 2 выигрывает у примера 1, потому что в нём внутренний цикл выполняется значительно быстрее: примерно на 33% при написании кода вручную и на 21% при использовании “компилятора с 90-процентной эффективностью” и подавленной проверкой границ, так что в обоих случаях устранение go to также приводит к значительному ускорению программы.
Эффективность
Соотношение полученных времён выполнения удивляет людей, не изучавших поведение программ. Пример 2 не выглядит настолько эффективным, насколько он им является. Опыт показывает (см. работы “The execution time profile as a programming tool”, “An empirical study of FORTRAN programs”), что большая часть ресурсов времени в программах, не упирающихся в ограничения ввода-вывода, сосредоточена примерно в 3% исходного текста. Часто в программе оказывается короткий внутренний цикл, эффективность которого в значительной степени определяет скорость работы всей программы. Ускорение внутреннего цикла на 10% ускоряет работу программы почти на 10%.
Мой собственный стиль программирования, конечно, изменился за последнее десятилетие в соответствии с общими тенденциями (например, я уже не так склонен к изобретательности и реже использую операторы go to), но главное изменение в моем стиле произошло благодаря этому феномену внутренних циклов. Теперь я пристально смотрю на каждую операцию в критическом внутреннем цикле, стремясь изменить свою программу и структуру данных так, чтобы некоторые из операций можно было вообще удалить (как было показано выше, при переходе от примера 1 к примеру 2).
Причины такого подхода в том, что:
- это не требует много сил и времени, поскольку внутренний цикл обычно короткий;
- результат моих действий реально ощутим;
- я могу позволить себе быть менее эффективным в других частях моих программ, которые от этого станут более читабельными и их будет легче писать и отлаживать. В настоящее время разрабатываются инструменты, облегчающие поиск критических мест в коде.
Если бы я не увидел, как убрать одну из операций из цикла в примере 1, перейдя к примеру 2, я бы сделал цикл for выполняющимся от m до 1, а не от 1 до m, поскольку обычно эффективнее проверить на ноль, чем сравнивать с m. А если бы требования к эффективности примера 2 были критичными, я бы ещё улучшил его, продублировав код:
Пример 2a:
A[m+1] := x; i := 1; go to test;
loop: i := i+2;
test: if A[i] = x then go to found fi;
if A[i+1] != then go to loop fi;
i := i+1;
found: if i > m then m := i; B[i] := 1;
else B[i] := B[i]+1 fi;
Здесь переменная цикла i увеличивается на 2 на каждой итерации, поэтому тело цикла выполняется в два раза меньше, чем раньше. Остальной код в цикле был, по сути, продублирован, чтобы это сработало. Такие оптимизации циклов несложно освоить, и, как я уже говорил, они уместны лишь в небольшой части программы, но очень часто дают существенную экономию. (Конечно, если мы захотим еще больше улучшить пример 2a, особенно при больших m, мы будем использовать более сложную технику поиска, но давайте пока не будем этого делать, поскольку я хочу проиллюстрировать оптимизацию циклов вообще, а не поиск в частности).
Прирост скорости при переходе от примера 2 к примеру 2a составляет около 12%, и многие сочтут это незначительным. Распространённое мнение заключается в игнорировании эффективности в мелочах, но я считаю, что это просто реакция на злоупотребления, практикуемые программистами, экономящими копейки и теряющими рубли, которые после череды микрооптимизаций теряют способность отлаживать или поддерживать свои “оптимизированные” программы. В инженерных дисциплинах легко достигаемое улучшение на 12% никогда не считается маргинальным, и я считаю, что такая же точка зрения должна преобладать и в программной инженерии. Конечно, я не стал бы заниматься подобными оптимизациями для одноразовой программы, но когда речь идет о разработке качественных программ, я не хочу ограничивать себя инструментами, которые лишают меня такой эффективности.
Несомненно, стремление к эффективности приводит к злоупотреблениям. Программисты тратят огромное количество времени, думая или беспокоясь о скорости выполнения некритичных частей своих программ, и эти попытки на самом деле оказывают сильное негативное влияние, когда речь заходит об отладке и поддержке. Мы не должны задумываться о мелких улучшениях где-то в 97% случаев: преждевременная оптимизация - это корень всех зол.
И всё же не стоит упускать возможности в тех критических 3%. Хороший программист не будет успокоен рассуждениями, он внимательно изучит критический код. Но только после того, как этот код будет обнаружен. Часто первые суждения о том, какие части программы действительно критичны, оказываются ошибочными. И опыт программистов, использующих измерительные инструменты, подтверждает, что предположения, основанные на интуиции, оказываются ложными. Проработав с такими инструментами семь лет, я мечтаю, чтобы все будущие компиляторы предоставляли программистам обратную связь, сообщая о самых нагруженных частях программ. Более того, эта обратная связь должна предоставляться всегда и автоматически. (Если, конечно, программист сам её не выключит)
После того как программист поймёт, какие части его процедур действительно важны, такое преобразование, как удвоение циклов, будет иметь смысл. Обратите внимание, что это преобразование вводит операторы go to - как и несколько других оптимизаций циклов (я вернусь к этому вопросу позже). Пока же я должен признать, что наличие операторов go to в примере 2a оказывает как отрицательное, так и положительное влияние на эффективность. Неоптимизирующий компилятор будет склонен выдавать корявый код, поскольку не сможет контролировать содержимое регистров при переходе по метке. Когда я вычислил приведённое выше время работы, посмотрев на вывод типичного компилятора для этого примера, я обнаружил, что улучшение производительности оказалось не таким значительным, как я ожидал.
Выходы при ошибках
Для простоты я обошел стороной очень важный вопрос в предыдущих примерах, но теперь про него придётся рассказать. Все рассмотренные нами программы демонстрируют плохую практику программирования, поскольку в них не выполняются проверки выхода за границы диапазона. Каждый раз, прежде чем выполнить команду “m := i”, мы должны сделать подобную проверку:
if m = max then go to memory overflow;
где max - соответствующее предельное значение. Я не включил эти проверки в примеры, чтобы не они не отвлекали внимание, но сейчас мы должны их рассмотреть, поскольку это ещё один важный класс операторов go to: выход при ошибках. Такие проверки очень важны, и, похоже, это тот класс применения go to, который ведущими реформаторами современности всё ещё считается уродливым, но необходимым. (Я удивляюсь, как Вэлу Шорре удавалось все эти годы избегать таких проверок).
Иногда необходимо выйти из нескольких уровней вложенности, пересекая код, который, возможно, даже был написан другими программистами, и самый изящный способ сделать это - прямой переход с помощью go to или его эквивалента. Тогда промежуточные уровни программы можно писать в предположении, что в них не возникнет ошибок.
Я вернусь позже к этой теме.
Проверка границ
В примерах, приведенных выше, мы, конечно, можем избежать сравнения m и max, если в компиляторе есть динамическая проверка всех индексов A. Но ошибка при такой проверке обычно прерывает программу, не давая нам практически никакого контроля над устранением ошибок, поэтому мы, вероятно, всё равно захотим проверить m. И, ох, как же проверка границ диапазонов влияет на время выполнения внутреннего цикла!.. В примере 2 я, конечно, захочу подавить проверку в конструкции while, поскольку в нём индексы не могут выйти за пределы, если только A[m+1] уже не был некорректным в предыдущей строке. Аналогично, в примере 1 в цикле for не может быть ошибки выхода за границы, если эта ошибка не случилась ранее. Кажется бессмысленным проводить дорогостоящие проверки в тех частях моих программ, в безопасности которых я уверен.
В этой связи я должен упомянуть почти убедительные аргументы Хоара. Он совершенно правильно отмечает, что нынешняя практика добавления проверок индексов в машинный код во время тестирования программы, а затем исключение этих проверок во время нормальной работы, похожа на моряка, который носит спасательный жилет во время тренировок на суше, но оставляет его дома, когда выходит в море! С другой стороны, этот моряк не так глуп, если спасательные жилеты крайне дороги и он настолько хорошо плавает, что вероятность потребности в жилете крайне мала, по сравнению с другими рисками, которым он подвергается. В приведенных выше примерах мы гораздо больше уверены в корректности индексов, чем в том, что другие аспекты нашей общей программы будут работать правильно. Джон Кок отмечает, что затратных проверок можно избежать с помощью умного компилятора, который сначала вкомпилирует проверки в программу, а затем вынесет их за пределы цикла. Вирт и Хоар отмечают, что хорошо разработанная реализация оператора for может позволить даже довольно простому компилятору избегать проверок внутри циклов.
Я считаю, что проверки границ должны использоваться гораздо чаще, чем сейчас, но в то же время, не везде. С другой стороны, говоря это, я рассчитываю, что в аппаратном обеспечении нет ошибок. Конечно, я бы не хотел удалять механизм контроля чётности из аппаратуры, даже при гипотетическом предположении, что она замедляет вычисления. Дополнительная защита памяти необходима для того, чтобы моя программа не повредила чужую, а чужая программа не испортила мою. Мои аргументы направлены на программные проверки, а не на аппаратные механизмы, которые действительно необходимы для обеспечения надёжности.
Хэши
Теперь рассмотрим другой пример, основанный на стандартной технике хэширования, но в остальном решающий ту же задачу, что и раньше. Здесь h(x) - это хэш-функция, принимающая значения от 1 до m при x != 0. В данном случае выберем m несколько большим числа элементов в таблице, а “пустые” позиции обозначим нулём.
Пример 3:
i := h(x);
while A[i] != 0 do
begin if A[i] = x then go to found fi;
i := i-1; if i = 0 then i := m fi;
end
not found: A[i] := x, B[i] := 0;
found: B[i] := B[i]+1;
Если мы проведём анализ, аналогичный тому, что мы сделали над примером 1, то увидим, что трюк, который нас привел к примеру 2, больше не работает. И всё же, если мы хотим избавиться от go to, мы можем применить идею примера 1a, записав:
while A[i] != 0 and A[i] != x do ...
и затем проверить, какое из условий вызвало завершение. Эта версия, возможно, немного проще для чтения, но, к сожалению, она добавляет избыточные проверки, которых мы хотели бы избежать, если находимся в критической части программы.
Почему я вообще беспокоюсь о лишней проверке в этом случае? В конце концов, дополнительная проверка того, был ли A[i] не 0 или не x, выполняется вне цикла while, а я говорил, что мы, как правило, должны ограничивать наши оптимизации только внутренними циклами. В данном случае причина в том, что этот цикл while чаще вообще не будет циклом: при правильном выборе h и m операция i := i-1 будет выполняться очень редко, в среднем менее одного раза за поиск. Таким образом, вся программа примера 3, за исключением, возможно, строки с меткой “not found”, должна рассматриваться как часть внутреннего цикла, если этот поиск является доминирующей частью общей программы. Поэтому дополнительная проверка в этом случае будет существенной.
Несмотря на мою заботу об эффективности, мне следовало бы написать первый вариант примера 3 без этого оператора go to, возможно, даже используя выражение while и расширение языка, например:
while A[i] not in {0, x} do ...
поскольку такая запись обобщает реальный смысл происходящего. Возможно, когда-нибудь появятся средства, способные проверить вхождение в небольшое множество более эффективно, чем последовательный перебор, и они сгенерируют лучший код, чем пример 3. Но есть и гораздо более веская причина, по которой мы предпочитаем эту форму while: она отражает симметрию между 0 и x, которой нет в примере 3. Например, если в реальном приложении окажется, что условие A[i] = x завершает цикл гораздо чаще, чем A[i] = 0, мы можем изменить программу:
Пример 3a:
i := h(x);
while A[i] != x do
begin if A[i] = 0
then A[i] := x; B[i] := 0;
go to found;
fi;
i := i-1; if i = 0 then i := m fi;
end;
found: B[i] := B[i]+1;
Её проще вывести из варианта без go to, чем из примера 3. И в то же время она лучше, чем пример 3. Таким образом, мы снова получили преимущество из откладывания оптимизаций до выяснения деталей о реальном использовании программы.
Продолжим рассмартривать пример 3a. Предположим, что теперь цикл while выполняется многократно в процессе поиска. И хотя в сценарии хэширования такого быть не должно, могут быть и другие программы с подобным циклом, поэтому рассмотрим, что следует делать в таких случаях. Если цикл while становится внутренним циклом, вся картина меняется. Избыточная проверка вне цикла становится совершенно незначительной, но проверка “if i = 0” внезапно приобретает большое значение. Как правило, мы хотим избежать проверки условий, которые почти всегда ложны, внутри критического цикла. Поэтому при этих новых предположениях я бы изменил структуру данных, добавив в массив новый элемент A[0] = 0 и убрал бы проверку на i = 0 следующим образом:
Пример 3b:
i := h(x);
while A[i] != x do
if A[i] != 0
then i := i-1
else if i = 0
then i := m;
else A[i] := x; B[i] := 0;
go to found;
fi;
fi;
found: B[i] := B[i]+1;
Теперь цикл работает ощутимо быстрее. И, да, я был бы недоволен медленной проверкой диапазонов, если бы этот цикл был критичным. Кстати, пример 3b был получен из примера 3a, а при применении той же идеи к примеру 3 получилась бы совсем другая программа. Тогда проверка if i = 0 добавилась бы вне цикла, в метку not found, и понадобился бы один оператор go to.
Как и в первых примерах, программа в примере 3 несовершенна: она не проверяет выход за границы. Я мог бы это исправить, например добавив счётчик n с количеством ненулевых элементов. Тогда процедура not found будет начинаться с чего-то вроде n := n+1; if n = m then go to memory overflow.
Сканирование текста
Впервые я осознанно применил методологию структурного программирования “сверху вниз” к достаточно сложной работе в середине 1972 года, когда писал программу для подготовки оглавления к своей книге “Сортировка и поиск”. Я был вполне доволен получившейся программой (в ней была только одна серьёзная ошибка), но я использовал один оператор go to. В том случае причина была чуть иной, не связанная с выходом из циклов. Я выходил из конструкции if-then-else.
Следующий пример представляет собой упрощённую версию проблемы, с которой я столкнулся.
Предположим, что мы обрабатываем поток текста и хотим прочитать и напечатать каждый следующий символ из входных данных. Однако, если этот символ - слэш “/”, мы хотим вместо этого сделать “табуляцию”, а два последовательных слэша означают “возврат каретки”. После печати точки “.” мы хотим вставить в вывод дополнительный пробел. Следующий код решает эту задачу “в лоб”:
Пример 4:
x := read char;
if x = slash
then x := read char;
if x = slash
then return the carriage;
go to char processed;
else tabulate;
fi;
fi;
write char (x);
if x = period then write char (space) fi;
char processed:
На практике мы сталкиваемся с ситуациями, когда цепочки принятия решений пишутся с помощью вложенных ветвей if-then-else, а затем две или более ветвей сливаются обратно в одну. Мы можем решать такие задачи на таблицах принятия решений, без go to, копируя общий код в каждое место, или определяя его как процедуру, но это не проще, чем перейти по go to в общую частью программы. Так, в примере 4 я мог бы избежать go to, скопировав write char (x); if x = period then write char (space) fi в программу после tabulate;. Но это была бы бессмысленная трата энергии только для того, чтобы устранить вполне понятный оператор go to. И полученную программу было бы сложнее поддерживать, чем прежнюю, поскольку теперь печать символа появляется в двух разных местах. Альтернатива с добавлением процедур позволяет избежать этой проблемы, но и она не ососбо привлекательна. Есть ещё вариант:
Пример 4a:
x := read char;
double slash := false;
if x = slash
then x := read char;
if x = slash
then double slash := true;
else tabulate;
fi;
fi;
if double slash
then return the carriage;
else write char(x);
if x = period then write char (space) fi;
fi;
На мой взгляд, получилось не лучше, чем в примере 4. Более того, может быть стало даже сложнее, потому что теперь вся процедура знает о специальной обработке правила “двойного слэша”, вместо того чтобы решать эту проблему в одном исключительном месте.
Признание
Прежде чем мы перейдем к другому примеру, я должен признаться в том, что многие читатели уже подозревают: я предвзят, и мне нужны операторы go to! Стиль серии книг “Искусство программирования”, которые я пишу, был задан в начале 1960-х годов, и мне было бы слишком сложно изменить его сейчас. Я представляю алгоритмы в своих книгах, используя неформальные описания на английском языке, и go to или его эквивалент - это почти единственная управляющая структура, которая у меня есть. Что ж, я оправдываю этот очевидный анахронизм тем, что:
- неформальное описание на английском языке кажется удачным решением, потому что многие читатели рассказывают, что легко читают по-английски, но пропускают код, написанный формально;
- когда операторы
go toиспользуются разумно вместе с комментариями, указывающими неочевидные инварианты цикла, они семантически эквивалентны операторамwhile. Разве что отсутствуют отступы для обозначения структуры; - алгоритмы у меня почти всегда короткие, так что сопровождающие блок-схемы могут проиллюстрировать их структуру;
- я стараюсь представить алгоритмы в форме, наиболее эффективной для реализации, а высокоуровневые структуры часто не дают такой возможности;
- многие читатели получат удовольствие от преобразования моих алгоритмов в красиво структурированные программы на формальном языке программирования;
- мы всё ещё не всё знаем о структурах управления, а я не могу позволить себе ждать окончательного консенсуса.
Несмотря на все эти рационализации, мне неуютно от того, что другие иногда публикуют примеры алгоритмов в “моём” стиле, но без важных комментариев или с безудержным использованием операторов go to. Кроме того, я и сам, бывало, использовал сложные структуры с множеством go to. Особенно в печально известном “Алгоритме 2.3.3A для сложения многочленов от нескольких переменных” (“Искусство программирования. Том 1”). В оригинальной программе было как минимум три ошибки, поэтому упражнение 2.3.3-14, “Приведите формальное доказательство (или опровержение) справедливости алгоритма A”, оказалось неожиданно лёгким. Теперь, во втором издании, я считаю, что пересмотренный алгоритм верен, но я всё ещё не знаю хорошего способа его доказать: мне пришлось повысить оценку сложности упражнения 2.3.3-14, и я надеюсь, что когда-нибудь этот алгоритм будет отполирован без потери эффективности. (прим: В 2014 вышла работа, доказывающая корректность исправленного алгоритма: “Provably Correct Derivation of Algorithms Using FermaT”)
В моих книгах особое внимание уделяется эффективности, поскольку в них рассматриваются алгоритмы, которые повторно используются в качестве строительных блоков для других программ. Но, как уже говорилось выше, эффективность важна к месту, и когда она становится важна, мы также должны знать, как ее достичь.
Чтобы можно было получить количественные оценки эффективности, в моих книгах показано, как анализировать программы на машинном языке. Эти программы написаны на MIXAL, придуманном мной языке ассемблера, который точно соответствует машинному коду, один-к-одному. В этом есть своя польза, но есть и опасность придания ассемблеру слишком большого значения. Программы на MIXAL, как и программы на машинном языке, лишены структуры, или, точнее, нам трудно там её разглядеть. Сопроводительные комментарии объясняют код и связывают его с глобальной структурой, показанной на блок-схемах. Но понять что происходит не так-то просто, и легко совершить ошибки, отчасти из-за того, что мы сильно доверяемся комментариям, среди которых могут быть и неточные описания работы программы. Лучше программировать на языке, который позволяет выразить структуру исполнения, даже если на каждом шаге мы будем задумываться об аппаратной реализации.
С другой стороны, я не очень расстроен программами на MIXAL в моих книгах, потому что считаю, что у меня получился хороший пример “быстрого и простого ассемблера”: жанра программного обеспечения, который всегда будет полезен в своей роли. Такой ассемблер характеризуется языковыми ограничениями, которые делают возможным его простую однопроходную реализацию, и он имеет несколько примечательных преимуществ, которые полезны при освоении новой машины:
- он сильно лучше, чем числовой машинный код;
- его правила легко сформулировать;
- его можно реализовать за пол дня, и быстро получить эффективный ассемблер, работающий на, возможно, очень примитивном оборудовании.
К настоящему моменту я написал уже шесть таких реализаций, для разных машин, интерпретируемых систем или микропроцессоров, на которых не было готового программного обеспечения сопоставимой полезности. И в каждом случае другие ограничения делали непрактичным тратить дополнительное время для разработки полноценного структурного ассемблера. Таким образом, я уверен, что концепция “ассемблера на скорую руку” полезна, и я рад, что MIXAL для этого подходит. Однако я также твердо убеждён, что подобные языки никогда не следует улучшать до такой степени, чтобы они стали слишком простыми или слишком приятными в использовании. Необходимо ограничить их примитивным оборудованием, на котором их легко реализовать эффективно. Я никогда не добавлю двухпроходный парсинг, сложные псевдооперации, макрофункции или даже хорошую диагностику ошибок, и не буду поддерживать или распространять такой язык в качестве стандартного инструмента программирования для реальной машины. Все подобные улучшения и усовершенствования должны быть в полноценном структурном ассемблере. Теперь, когда технологии стали позволять, мы должны применять неструктурные языки только в качестве вспомогательного средства для достижения конкретной ограниченной цели, когда есть веские экономические причины отказа от внедрения лучшей системы.
Поиск в дереве
Но я отвлёкся от темы исключения операторов go to из языков высокого уровня. Несколько недель назад я решил выбрать наугад какой-нибудь алгоритм из своих книг, чтобы изучить, как в нём используются операторы go to. Первый же пример, с которым я столкнулся, оказался ещё одним случаем, когда существующие языки программирования не имеют хорошей замены для go to. В упрощённом виде цикл, в котором возникают сложности, можно записать следующим образом:
Пример 5
compare:
if A[i] < x
then if L[i] != 0
then i := L[i]; go to compare;
else L[i] := j; go to insert fi;
else if R[i] != 0
then i := R[i]; go to compare;
else R[i] := j; go to insert fi;
fi;
insert: A[j] := x;
L[j] := 0; R[j] := 0; j := j+1;
Это часть общеизвестного алгоритма “поиска и вставки”, в которой двоичное дерево поиска представлено тремя массивами: A[i] обозначает информацию, хранящуюся в узле под номером i, а L[i], R[i] - соответствующие номера узлов для корней левого и правого поддеревьев этого узла. Пустые поддеревья обозначаются нулём. Программа ищет по дереву, пока не найдёт пустое поддерево, в которое можно вставить x. Переменная j указывает на соответствующее место для вставки. Для удобства, в этом примере я предположил, что x ещё не присутствует в дереве поиска.
В примере 5 есть четыре оператора go to, но структура выполнения очевидна, потому что программа абсолютно симметрична между L и R. Я знаю, что эти операторы go to можно устранить, добавив булеву переменную, которая становится true, когда L[i] или R[i] оказываются равными нулю. Но я не хочу проверок этой переменной во внутреннем цикле программы.
Систематическое удаление
Вопросу о удаления go to было посвящено много теоретических работ, и я попытаюсь обобщить их результаты и оценить их актуальность.
Якопини в 1966 году в работе, написанной совместно с К. Бомом показал, что любая программа, представленная, скажем, в виде блок-схемы, может быть системно преобразована в другую программу, которая выдаёт те же результаты и которая строится из утверждений исходной программы с использованием только трёх основных операций: композиции, условия и цикла, плюс возможных операторов присваивания и проверок с помощью дополнительных переменных. Таким образом, в принципе, операторы go to всегда можно удалить. Подробное изложение конструкции Якопини было дано Х. Д. Миллсом (“Математические основы структурированного программирования”).
Недавний интерес к структурному программированию заставил многих авторов ссылаться на результат Якопини как на значительный прорыв и краеугольный камень современной техники программирования. К сожалению, эти авторы не знают о замечаниях, сделанных Купером в 1967 году и позже Бруно и Штейглицем, а именно, что с практической точки зрения эта теорема бессмысленна. Действительно, любая программа может быть приведена к “красиво структурированной” форме:
p := 1;
while p > 0 do
begin if p = 1 then perform step 1;
p := successor of step 1 fi;
if p = 2 then perform step 2;
p := successor of step 2 fi;
. . .
if p = n then perform step n;
p := successor of step n fi;
end
Здесь вспомогательная переменная p служит счётчиком, указывающим, в каком блоке блок-схемы мы находимся, и программа останавливается, когда p устанавливается в ноль. Мы устранили все операторы go to, но на самом деле потеряли всю структуру.
Якопини высказал в своей статье предположение, что вспомогательные переменные необходимы в общем случае, и что операторы go to в программе следующего вида:
L1: if B1 then go to L2 fi;
S1;
if B2 then go to L2 fi;
S2;
go to L1;
L2: S3;
не всегда можно удалить, если не вводить дополнительных вычислений. Мы с Флойдом и Джоном Хопкрофтом доказали эту гипотезу.
Оригинальная конструкция Якопини не была просто тривиальным алгоритмом для эмуляции блок-схем, она позволяет сохранить большую часть оригинальной хорошей управляемой структуры. Более общая техника удаления go to, разработанная Эшкрофтом и Манной, ещё сильнее контролирует естественный поток выполнения программы. Например, их подход, примененный к примеру 5, даёт:
Пример 5a:
t := true;
while t do
begin if A[i] < x
then if L[i] != 0 then i := L[i];
else L[i] := j; t := false fi;
else if R[i] != 0 then i := R[i];
else R[i] := j; t := false fi;
end;
A[j] := x;
Но в целом такая техника может привести к экспоненциальному росту размера программы, а при наличии переходов при обработке ошибок или других “неудобных” go to, результирующие программы будут похожи на эмулятор блок-схемы, приведённый выше.
Если такие автоматические процедуры устранения go to применяются к плохо структурированным программам, можно ожидать, что результирующие программы будут, как минимум, такими же плохо структурированными.
Другими словами, мы не должны просто удалять операторы go to, потому что это модно. Наличие или отсутствие операторов go to на самом деле не является проблемой. Главное - это структура программы, и мы хотим лишь избежать её загромождения. Хорошая структура может быть выражена и на FORTRAN, и на COBOL, или даже на языке ассемблера, хотя и менее чётко и со значительно большим трудом. Настоящая цель - сформулировать наши программы таким образом, чтобы их было легко понять.
Под структурой программы понимается способ, которым сложный алгоритм строится из последовательно выполняемых более простых процессов. В большинстве ситуаций эта структура может быть очень хорошо описана в терминах последовательной композиции, условных обозначений, циклов и операторов case для сложных ветвлений. Беспорядочные операторы go to делают структуру программы более сложной для восприятия, и они часто являются маркерами концептуально плохого решения. Однако в последнее время слишком много внимания уделяется устранению go to, а не действительно важным вопросам: люди имеют естественную тенденцию ставить перед собой легко понимаемую количественную цель, например, отказ от переходов, вместо того, чтобы работать непосредственно над качественной целью, например, хорошей структурой программы.
Вероятно, худшая ошибка, которую можно совершить в связи с темой операторов go to - это предположить, что “структурное программирование” достигается путём написания программы как обычно, а затем устранением операторов go to. Большинство операторов go to вообще не должны быть написаны! На самом деле мы хотим создавать программу таким образом, чтобы редко вспоминать об операторах go to, потому что реальной необходимости в них почти никогда не возникает. Язык, на котором мы выражаем свои идеи, оказывает сильное влияние на наш мыслительный процесс. Поэтому Дейкстра и выступает за добавление новых языковых конструкций, чтобы чётче выражать свои намерения и избежать усложнения кода при удалении go to.
Индикаторы событий
Лучшая из известных мне возможностей языка была недавно предложена К. Т. Заном. Поскольку эта работа всё ещё находится на стадии эксперимента, я возьму на себя смелость немного модифицировать предложенный “синтаксический сахар”, не изменяя основной идеи. Существенная новизна его подхода заключается во введении в языки программирования новой величины, называемой индикатором события. Я пишу его событийно-управляемую конструкцию в двух общих формах:
А)
loop until <event>1 or ... or <event>n:
<statement list>0;
repeat;
then <event>1 => <statement list>1;
⋮
<event>n => <statement list>n;
fi;
Б)
begin until <event>1 or ... or <event>n;
<statement list>0;
end;
then <event>1 => <statement list>1;
⋮
<event>n => <statement list>n;
fi;
Новая конструкция <event> означает, что указанное событие произошло: такое утверждение разрешено только в списке <statement list>0 в конструкции until внутри которой объявляется это событие.
В форме (А) <statement list>0 выполняется многократно, пока управление не выйдет из цикла или пока не произойдёт одно из указанных событий. В последнем случае выполняется список операций, соответствующих этому событию. Поведение в форме (Б) аналогично, за исключением того, что цикла не подразумевается вовсе: какое-то событие должно произойти до достижения end. Часть then ... fi может быть опущена, если событие может быть только одним единственным.
Чтобы стало понятнее, приведу пример 5, изменённый с применением этой новой возможности:
Пример 5b:
loop until left leaf hit or right leaf hit:
if A[i] < x
then if L[i] != 0 then i := L[i];
else left leaf hit fi;
else if R[i] != 0 then i := R[i];
else right leaf hit fi;
fi;
repeat;
then left leaf hit => L[i] := j;
right leaf hit => R[i] := j;
fi
A[j] := x; L[j] := 0; R[j] := 0; j := j+1;
Или используя одно событие,
Пример 5c:
loop until leaf replaced:
if A[i] < x
then if L[i] != 0 then i := L[i]
else L[i] := j; leaf replaced fi;
else if R[i] != 0 then i := R[i]
else R[i] := j; leaf replaced fi;
fi;
repeat
A[j] := x; L[j] := 0; R[j] := 0; j := j+1;
По причинам, которые рассмотрим позже, пример 5b предпочтительнее, чем 5c.
Важно подчеркнуть, что в первой строке конструкции просто объявляются имена индикаторов событий и что индикаторы событий не являются условиями, которые постоянно проверяются. Операторы <event> - это только описания передачи управления, которую компилятор может обрабатывать очень эффективно. Так, в примере 5c выражение leaf replaced по сути является оператором go to, который выходит из цикла.
Такое использование событий семантически эквивалентно ограниченной форме оператора go to, про которую Питер Лэндин рассказывал в 1965 году, ещё до того, как большинство из нас были готовы слушать. Подход Лэндина был переформулирован Клинтом и Хоаром следующим образом:
Метки объявляются в начале каждого блока, как обычно объявляются процедуры, и каждая метка имеет тело <label body>, так же, как и процедура имеет тело <procedure body>. Внутри блока, в заголовке которого содержится объявление метки L, оператор go to L, согласно этой схеме, означает “выполнить тело L, затем выйти из блока”. Легко видеть, что это именно та форма управления, которую обеспечивает событийный механизм Зана, где конструкции <label body>, заменены на <statement list> в then ... fi, и добавлены операторы <event>, соответствующие операторам go to у Лэндина. Таким образом, Клинт и Хоар написали бы пример 5b в следующем виде:
while true do
begin
label left leaf hit; L[i] := j;
label right leaf hit; R[i] := j;
if A[i] < x
then if L[i] != 0 then i := L[i];
else go to left leaf hit fi;
else if R[i] != 0 then i := R[i];
else go to right leaf hit fi;
end;
A[j] := x:; L[j] := 0; R[j] := 0; j := j+1;
Мне больше нравится программа с <label body> расставленными по коду в соответствующих местах.
Лэндин также добавил в свои “метки” возможность передачи параметров, как и в процедуры. Это ценное расширение предложения Зана, поэтому я буду использовать события с параметрами значений в примерах ниже.
Как показал Зан, событийно-ориентированные выражения хорошо сочетаются с идеями структурного программирования путем пошагового уточнения. Так, примеры 1-3 можно привести к следующей более абстрактной форме, используя событие found с целочисленным параметром:
begin until found:
search table for x and insert it if not present;
end;
then found (integer j) => B[j] := B[j]+1;
fi;
Эта часть программы может быть написана ещё до принятия решения о том, как будет устроено хранение данных. На следующем уровне абстракции мы можем решить использовать последовательный список, как в примере 1, так что search table ... превратится в:
for i := 1 step 1 until m do
if A[i] = x then found(i) fi;
m := m+1; A[m] := x; found(m);
Обратите внимание, что этот цикл for более строгий, чем тот, что был в нашем исходном примере 1, поскольку переменная итерации не используется вне цикла. Теперь он соответствует правилам ALGOL W и ALGOL 68. Такие циклы for документируют сам код и позволяют избежать распространенных ошибок, связанных с глобальными переменными.
Аналогично, если мы хотим использовать идею примера 2, мы можем написать следующее, как развитие “search table ...”:
begin integer i;
A[m+1] := x; i := 1;
while A[i] != x do i := i+1;
if i > m then m := i; B[m] := 0 fi;
found(i);
end;
И, наконец, если мы решим использовать хэширование, то получим эквивалент примера 3, который можно записать так:
begin integer i;
i := h(x);
loop until present or absent:
if A[i] = x then present fi;
if A[i] = 0 then absent fi;
i := i-1;
if i = 0 then i := m fi;
repeat;
then present => found(i);
absent => A[i] := x; found(i);
fi;
end;
Конструкция begin until <event> обеспечивает естественный способ работы с таблицами принятия решений, такими, как рассмотренное выше приложение для разбора текста. Эта программа описывает действия чуть более явно, чем все наши предыдущие попытки:
Пример 4b:
begin until normal character input or double slash:
char x;
x := read char;
if x = slash
then x := read char;
if x = slash
then double slash;
else tabulate;
normal character input (x);
fi;
else normal character input (x);
fi;
end;
then normal character input (char x) =>
write char (x);
if x = period then write char (space) fi;
double slash => return the carriage;
fi;
Индикаторы событий также подходят и для обработки ошибок. Например, мы можем написать программу следующим образом:
begin until error or normal end:
...
if m = max then error ('symbol table full') fi;
...
normal end;
end;
then error (string S) =>
print ('unrecoverable error,', S);
normal end =>
print ('computation complete');
fi;
Сравнение возможностей
Конечно, индикаторы событий - не единственная достойная альтернатива операторам go to. Многие авторы предложили функции языка, которые обеспечивают примерно эквивалентные возможности, но выражаются в терминах операторов exit, jumpout, break или leave. Косараджу доказал, что наличия подобных операторов достаточно для написания всех программ без операторов go to и без каких-либо дополнительных вычислений, но только если будет возможно прерывать работу произвольно большого количества уровней вложенности.
Более ранние языковые средства такого рода (помимо предложения Лэндина) предусматривали ровно один выход из цикла. Это означает, что код, появляющийся в then ... fi наших примеров, вставлялся бы в само тело перед ветвлением (см. пример 5c). Разделение такого кода, как в предложении Зана, лучше, главным образом потому, что каждому событию соответствует определенный набор утверждений о состоянии программы, и код, который следует за этим событием, учитывает эти утверждения, которые довольно сильно отличаются от утверждений в основном теле конструкции. (По этой причине я предпочитаю пример 5b примеру 5c).
Особенности языка, реализующие множественные точки выхода, были предложены Бохманом и независимо от него Шиго и другими. Они семантически почти эквивалентны предложениям Зана, но выражают такую семантику в терминах утверждений: exit to <label>. Я считаю, что идея Зана об индикаторах событий является улучшением по сравнению с предыдущими схемами, поскольку спецификация событий вместо меток способствует лучшему пониманию программы. Идентификатор, присваиваемый метке, часто представляет собой императивный глагол типа insert или compare, говорящий о том, какое действие должно быть выполнено дальше, в то время как подходящим идентификатором для события, скорее всего, будет прилагательное, типа found. Имена событий очень похожи на имена для булевых переменных, и я считаю, что именно этим объясняется их популярность в качестве вспомогательных средств документирования, несмотря на их неэффективность.
Проще говоря, с точки зрения психологии гораздо лучше написать:
loop until found ... ; found; ... repeat
чем:
search: while true do
begin ... ; leave search; ... end.
Операторы leave или exit хотя и делают одно и то же, но интуитивно воспринимаются по-разному, поскольку они больше описывают программу, а не решаемую ей проблему.
Некоторые предлагают, что “события” лучше было бы назвать “условиями” по аналогии с булевыми выражениями. Однако такая терминология будет подразумевать выражение, значение которого постоянно проверяется, а не событие. Написав loop until yprime is near y: ..., мы, вероятно, хотим сказать, что машина должна следить за тем, сошлись ли значения y и yprime. Более удачным выбором слов было бы название события типа loop until convergence established: ..., тогда мы можем написать if abs(yprime - y) < epsilon × y then convergence established. Событие возникнет, когда программа обнаружит, что результат вычислений изменился.
(прим: синтаксис вида leave search - это именно то, что в настоящий момент (2024) предлагает добавить Саттер в свой Cpp2)
Простые циклы
По моему мнению, самым распространённым случаем, когда операторы go to необходимы программисту на ALGOL или PL/I - это для реализации простого цикла с одним входом и одним выходом. В качестве альтернативы операторам go to чаще всего предлагаются операторы while B do S и repeat S; until B. Однако, на практике, циклы, с которыми я сталкиваюсь, часто имеют вид:
A: S;
if B then go to Z fi;
T; go to A;
Z:
где S и T представляют собой достаточно длинные куски кода. Если S пуст, то получится цикл while, а если T пуст, то repeat, но в общем случае, если убрать тут go to - это приведёт к неудобству.
Типичный пример такого цикла: S - это код для получения или генерации новой порции данных, B - проверка на конец данных, а T - их обработка.
Другой пример: код, предшествующий циклу, задаёт начальные условия для некоторого итерационного процесса, и S - это вычисление величин, участвующих в тесте на сходимость, B - тест на сходимость, а T - настройка переменных для следующей итерации.
Дейкстра метко назвал это циклом, который выполняется n + 1/2 раз. Обычная практика отказа от go to в таких циклах состоит в том, чтобы либо продублировать код для S, написав:
S; while Bn do begin T; S end;
где Bn - условие, обратное B. Или придумать что-то вроде “инверсии” для действия T, чтобы “Ti; T” было эквивалентно пустому выражению, и записать:
Ti; repeat T; S until B;
или продублировать код для B и написать лишнюю проверку:
repeat S; if Bn then T fi; until B;
или эквивалентную. Читатель, обращающий внимание на программы без go to, появляющиеся в литературе, уже заметил, что эти три неуклюжие конструкции используются довольно часто.
Я рассмотрел этот недостаток ALGOL в письме к Никлаусу Вирту в 1967 году, и он предложил два решения проблемы. А потом в докладе об основных концепциях языков программирования добавил ещё несколько. Его первое предложение заключалось в том, чтобы написать:
repeat begin S; when B exit; T; end;
и второе:
turn on begin S; when B drop out; T; end.
Ни один из вариантов, конечно, не идеален, но модификация первого предложения (разрешающая один или несколько одноуровневых операторов exit внутри repeat begin ... end) была позже включена в экспериментальную версию языка ALGOL W. Другие языки, такие как BCPL и Bliss заимствовали и расширили идею exit по примеру, описанному выше. Конструкция Зана теперь позволяет написать:
loop until all data exhausted:
S;
if B then all data exhausted fi;
T;
repeat;
и это лучший синтаксис для проблемы n + 1/2, чем тот, который был у нас ранее.
С другой стороны, было бы ещё лучше, если бы наш язык предоставлял способ описания цикла, не прибегая к таким мощным возможностям, как событийно-управляемая модель. Когда программист использует простую конструкцию, он тем самым даёт понять, что у него тут самый обычный цикл, с одним условием, которое проверяется ровно один раз на каждой итерации. Более того, предоставляя специальный синтаксис для этого общего случая, мы облегчим компилятору создание более эффективного кода, поскольку компилятор сможет перестроить машинные инструкции таким образом, чтобы проверка физически оказалась в конце цикла. (Каждый день многие часы компьютерного времени впустую тратятся на выполнение безусловных переходов в начало циклов).
Оле-Йохан Даль недавно предложил синтаксис, который, как мне кажется, является первым реальным решением проблемы n + 1/2. Он предлагает писать простой цикл, определёный выше, в виде:
loop; S; while Bn: T; repeat;
где, как и раньше, S и T обозначают последовательности из одного или нескольких выражений, разделенных точками с запятой. Обратите внимание, что, как и в двух наших оригинальных примерах без go to, синтаксис основан на условии Bn, которое обозначает необходимость продолжения, а не B, которое обозначает выход. Возможно, именно поэтому у него и получилось прийти к этому варианту.
Синтаксис Даля на первый взгляд может показаться плохим, но на самом деле он хорошо понятен в каждом примере, который я пробовал, и я надеюсь, что читатель воздержится от суждений, пока не увидит примеры далее в статье. Одно из приятных свойств такого синтаксиса заключается в том, что слово repeat находится в конце цикла, а не в его начале, и это удобно, поскольку мы читаем действия программы последовательно. Дойдя до конца, мы получаем указание повторить цикл, вместо того чтобы сообщить, что текст цикла (а не его выполнение) закончился. Кроме того, приведенный выше синтаксис позволяет избежать использования в ALGOL слова do (а также неестественного разделителя od). Слово do, используемое в ALGOL, всегда складывалось в странные конструкции для носителей английского языка: do read (A[i]) или do begin!
Самое приятное в предложении Даля - это то, что оно работает и тогда, когда S или T пусты, так что у нас есть единый синтаксис для всех трёх случаев. Операторы while и repeat, встречавшиеся в ALGOL-подобных языках конца 1960-х годов, больше не нужны. Когда S или T пусты, можно просто удалить предшествующий разделитель. Таким образом:
loop while Bn:
T;
repeat;
заменяет собой “while Bn do begin T end;” и
loop:
S
while Bn repeat;
заменяет “repeat S until B;”. На первый взгляд эти выражения могут показаться странными, но, вероятно, не более странными, чем операторы while и repeat сами по себе для неподготовленного новичка.
Если бы я разрабатывал язык программирования сегодня, я бы предпочел использовать механизм Даля для простых циклов, и более общую конструкцию Зана, и оператор for, синтаксис которого был бы чем-то подобным:
loop for 1 <= i <= n:
S;
repeat;
Эти управляющие структуры вместе с if ... then else ... fi позволят легко справиться со всеми примерами, рассмотренными до сих пор в этой статье, без каких-либо операторов go to и потери эффективности или ясности. Более того, ни одна из этих особенностей языка не способствует чрезмерному усложнению структуры программы.
2. Добавление операторов go to
До сих пор я рассказывал о том, как удалять операторы go to, но сейчас я покажу случаи, когда я наоборот, хочу добавить их в программу без go to. Дело в том, что я люблю легкочитаемые программы, но совершенно не люблю неэффективные. И в некоторых случаях мне просто необходимы операторы go to, несмотря на примеры, приведённые выше.
Удаление рекурсии
Такие случаи возникают, в основном, при попытке соптимизировать программу (изначально хорошо структурированную) и удалить явную или неявную рекурсию. Например, рассмотрим следующую рекурсивную процедуру, которая печатает содержимое бинарного дерева в симметричном порядке. Дерево представлено массивами L, A и R, как в примере 5, а рекурсивная процедура, по сути, является определением симметричного порядка.
Пример 6:
procedure treeprint(t); integer t; value t;
if t != 0
then treeprint(L[t]);
print(A[t]);
treeprint(R[t]);
fi;
Эту процедуру можно рассматривать как модель для множества алгоритмов, имеющих ту же структуру, поскольку обход деревьев встречается во многих приложениях. Пока что мы будем считать, что наша цель - печать, понимая, что это лишь один из примеров общего семейства алгоритмов.
Часто бывает полезно удалить рекурсию из алгоритма, чтобы сэкономить место или время, хотя это, как правило, приводит к некоторой потере ясности программы. (И, конечно, бывает нужно изложить наш алгоритм на языке типа FORTRAN или в машинном коде, где нет рекурсии). Даже если мы используем ALGOL или PL/I, каждый известный мне компилятор добавляет значительные накладные расходы на вызовы процедур. Это в определенной степени неизбежно из-за общности механизмов передачи параметров и поддержания надлежащего динамического окружения. Когда вызовы процедур происходят во внутреннем цикле, эти накладные расходы могут замедлить работу программы в два и более раз. Но если мы вручную пишем свою собственную реализацию рекурсии, а не полагаемся на общий механизм, то обычно можем найти достойные упрощения и в результате иногда получаем более глубокое понимание работы алгоритма.
Об устранении рекурсии опубликовано немало работ, но меня поражает, что очень мало из них посвящено проблемам из реальной жизни. Я всегда считал, что преобразование рекурсии в цикл - одна из самых фундаментальных концепций информатики и что студент должен изучать её примерно в то же время, когда он изучает структуры данных. Этой теме посвящена глава 8 в моем многотомном труде, и только по случайности рекурсия не стала главой 3: материал просто не поместился ни в один из предыдущих томов. Тем не менее в главах 1-7 есть множество алгоритмов, которые являются замаскированными рекурсиями. Поэтому меня удивляет, что литература по удалению рекурсий в основном посвящена “детским” примерам вроде вычисления факториалов или разворачивания списков, а не реальным задачам вроде примера 6.
Теперь приступим к работе над приведенным выше примером. Я полагаю, что читатель знает стандартный способ реализации рекурсии через стек, но я не хочу этим ограничиваться. Правило номер один для упрощения вызовов процедур таково: “Если последним действием процедуры p перед ее возвратом является вызов процедуры q, просто перейдите к началу процедуры q”. (На время забудем, что нам не нравятся операторы go to.)
В справедливости этого правила легко убедиться, если для простоты предположить, что процедуры не имеют параметров. Ведь операция вызова q состоит в том, чтобы поместить адрес возврата в стек, затем выполнить q, затем вернуться к p по указанному адресу возврата, затем вернуться к коду, вызывающему p. Вышеприведённое упрощение превращает q в продолжение вызова p. Когда q = p, этот аргумент, возможно, слабоват, но это ничего не меняет.
Я не уверен, что знаю, кто придумал этот принцип. Я прочёл о нём в работе Гилла, а затем видел много примеров использования в реализациях компиляторов. При определённых условиях компилятор Bliss/11 способен сам произвести такое упрощение. Кстати, верно и обратное утверждение: операторы go to всегда можно устранить, объявив подходящие процедуры, каждая из которых вызывает другую в качестве последнего действия. При этом нельзя утверждать, что процедуры концептуально проще операторов go to, хотя некоторые люди и заявляют подобное.
В результате применения указанного преобразования, и его адаптации к случаю процедуры с одним параметром, пример 6 приобретает вид:
Пример 6a:
procedure treeprint(t); integer t; value t
L: if t != 0
then treeprint(L[t]);
print(A[t]);
t := R[t]; go to L;
fi;
go to здесь особо не нужен, поэтому мы можем написать код следующим образом, используя синтаксис Даля для циклов:
Пример 6b:
procedure treeprint(t); integer t; value t;
loop while t != 0:
treeprint(L[t]);
print (A[t]);
t := R[t];
repeat;
Если мы захотим произвести на кого-то впечатление, можно сказать, что сразу придумали пример 6b, а не получили его путём упрощения тривиальной программы из примера 6.
В примере 6b всё ещё есть рекурсивный вызов, и на этот раз он встроен в процедуру, так что кажется, что без стека тут не обойтись. Однако рекурсивный вызов теперь происходит только в одном месте, и поэтому нам не нужно сохранять адрес возврата: при каждом вызове достаточно положить в стек только локальную переменную t. Тогда программа принимает следующий нерекурсивный вид:
Пример 6c:
procedure treeprint(t); integer t; value t;
begin integer stack S; S := empty;
L1: loop while t != 0:
S <= t; t := L[t]; go to L1;
L2: t <= S;
print(A[t]);
t := R[t];
repeat
if nonempty(S) then go to L2 fi;
end.
Здесь для простоты я добавил в ALGOL тип данных “стек”, где S <= t означает “поместить t на вершину S”, а t <= S означает “изъять вершину S в t, предполагая, что S не пустой”.
Легко видеть, что пример 6c эквивалентен примеру 6b. Оператор go to L1 начинает процедуру, а по её завершении управление возвращается к следующему оператору (помеченному L2). Хотя в примере 6c присутствуют операторы go to, их назначение легко понять, зная, что мы получили пример 6c с помощью механического, абсолютно надёжного метода удаления рекурсии. Хопкинс привёл и другие примеры, когда добавление go to на низком уровне позволяет поддержать высокоуровневые конструкции.
Но если вы ещё раз посмотрите на приведенную выше программу, вы, вероятно, будете так же потрясены, как и я, когда впервые осознал, что произошло. Я считал, что использование операторов go to - это плохо, но есть один вид go to, который считается вообще непростительным и смертным грехом: переход в середину цикла! Пример 6c именно таков, и при этом он прост, если сравнивать с примером 6b. В этом конкретном случае мы можем удалить go to без труда, но в общем случае, когда рекурсивный вызов встроен в несколько сложных уровней управления, не существует столь же простого способа удалить рекурсию, не прибегая к чему-то вроде примера 6c. Как я уже сказал, когда я впервые столкнулся с таким примером, это был шок. Позже Джим Хорнинг признался мне, что он тоже “сделал плохо” в программе построения синтаксических таблиц для системы XPL, потому что XPL не допускает рекурсии. Очевидно, что нам необходима новая доктрина о “плохих поступках”. Своего рода “ситуационная этика”.
Новая мораль, которую я предлагаю, может быть сформулирована следующим образом: “Определённые операторы go to, возникающие в связи с хорошо понятными преобразованиями, допустимы при условии, что из кода программы понятно, что это за преобразования”. Использование слова из четырех букв, такого как goto, иногда может быть оправдано даже в самой лучшей компании.
Эта ситуация очень похожа на ту, с которой люди часто сталкиваются при доказательстве корректности программы. Чтобы продемонстрировать корректность типичной программы Q, обычно проще и легче доказать, что некоторая довольно простая, но не очень эффективная программа P корректна, а затем доказать, что P может быть преобразована в Q с помощью последовательности допустимых оптимизаций. Я хочу сказать, что подобное должно считаться стандартной практикой для всех программ, кроме совсем уж простейших.
Программист сначала пишет программу P, которая понятна и легко читается, и только затем начинает оптимизировать её до крайне эффективной программы Q. Программа Q может содержать операторы go to и другие низкоуровневые функции, но преобразование из P в Q должно быть выполнено с помощью абсолютно надёжных и хорошо документированных “механических” операций.
На этом месте многие не согласятся и скажут: “Но достаточно написать только P, а оптимизирующий компилятор сам выдаст Q”. На что я отвечу: “Нет, оптимизирующий компилятор получится настолько сложным (намного сложнее, чем все программы, которые есть у нас сейчас), что он не будет надёжным”. У меня есть предложение получше: ввести новый класс программного обеспечения.
Системы преобразования программ
Уже 15 лет я пытаюсь придумать, как сделать компилятор, который бы действительно производил высококачественный код. Например, код большинства программ Mix в моих книгах значительно эффективнее, чем код, который может создать любая из самых современных систем компиляции. Я пытался изучить различные техники, которые использует ручной кодер вроде меня, и уложить их в некую систематическую и автоматическую систему. Несколько лет назад мы с несколькими студентами рассмотрели типичную выборку программ на языке FORTRAN и пытались понять, как машина может создать код, способный конкурировать с нашими лучшими программами, оптимизированными вручную. Мы постоянно натыкались на одно и то же: компилятор должен вести диалог с программистом. Он должен знать свойства данных, знать, могут ли возникать определенные случаи, и т. д. Мы так и не смогли придумать хороший язык, на котором можно было бы вести такой диалог.
По какой-то причине у всех нас (особенно у меня) был ментальный блок в отношении оптимизации: мы всегда считали её закулисной деятельностью, которая должна выполняться на машинном языке. Но ведь программист его совершенно не обязан знать. Эта завеса впервые была снята с моих глаз осенью 1973 года, когда я наткнулся на замечание Хоара о том, что в идеале язык должен быть разработан так, чтобы оптимизирующий компилятор мог описывать свои оптимизации прямо на исходном языке. Ну конечно! Почему я не подумал об этом?!
Когда у нас будет подходящий язык, мы сможем получить систему программирования будущего: интерактивную среду управления программами, аналогичную многим системам обработки символов, которые в настоящее время находятся в стадии активного развития и экспериментирования. Мы постепенно изучаем способы преобразования программ, которые сложнее, чем манипуляции с математическими формулами, но в действительности не сильно-то и отличаются.
Система преобразования программ - это, очевидно, то, к чему мы идём, и я удивляюсь, почему я не думал об этом раньше. Конечно, эта идея не принадлежит мне: когда я рассказал о ней Хоару, он сказал: “Вот именно!” и отослал меня к недавней работе Дарлингтона и Берстолла. В их работе описывается система, которая удаляет некоторые рекурсии из языка, похожего на LISP (любопытно, что при этом она не добавляет какие-либо go to), а также выполняет некоторые преобразования структур данных и реструктуризацию программы путём объединения похожих циклов. Появились и другие работы, посвящённые оптимизациям исходного кода. А поскольку программами на языке LISP легко манипулировать как объектами данных языка LISP, в этой области также ведётся довольно активная разработка аналогичных идей. Приходит время для создания систем преобразования программ, и впереди ещё много работы.
Программист, использующий такую систему, напишет свою красиво структурированную, но, возможно, неэффективную программу P, затем в интерактивном режиме укажет преобразования, которые сделают ее эффективной. Такая система будет гораздо более мощной и надёжной, чем полностью автоматическая. Представьте себе систему, оперирующую со статистикой того, какая часть общего времени выполнения приходится на каждое выражение: программист захочет знать, какие части его программы заслуживают оптимизации и какой эффект будет иметь оптимизация. Исходная программа P должна быть сохранена вместе со спецификациями проведённых преобразований, чтобы её можно было правильно понять и поддерживать с течением времени. Как я уже сказал, эта идея, конечно, не моя, но она настолько интересна, что я думаю, скоро все заговорят о её возможностях.
Формируется новая область знания: наборы действий, которые можно применять к программам, не переосмысливая каждый раз конкретную задачу. Я уже упоминал несколько таких преобразований: удвоение циклов (пример 2a), замена конечных вызовов на go to (пример 6a), использование стека для рекурсий (пример 6c), объединение разнородных циклов…
Другой хороший пример - удаление константных подвыражений из циклов. Общеизвестно, что программа, включающая такие выражения, более читабельна, чем соответствующая программа с выражениями, вынесенными за пределы циклов. Тем не менее мы сознательно выносим их, когда большое значение приобретает время работы программы.
Еще один тип преобразований - это переход от высокоуровневых “абстрактных” структур данных к конкретным низкоуровневым. В случае примера 6c мы можем заменить стек массивом и указателем, получив в результате:
Пример 6d:
procedure treeprint(t), integer t, value t;
begin integer array S[1:n]; integer k; k := 0;
L1: loop while t != 0:
k := k+1; S[k] := t;
t := L[t]; go to L1;
L2: t := S[k]; k := k-1;
print(A[t]);
t := R[t];
repeat;
if k != 0 then go to L2 fi;
end.
Здесь программист должен указать безопасное значение максимального размера стека n, чтобы преобразование было корректным. В качестве альтернативы он может захотеть реализовать стек в виде связанного списка. Этот выбор обычно не вызывает затруднений, но он иллюстрирует ещё одну область, в которой диалог предпочтительнее полностью автоматических преобразований.
Рекурсия или цикл
Прежде чем оставить в покое пример с деревом, я хотел бы рассмотреть вопрос об удалении go to из примера 6c, поскольку это приводит к некоторым интересным проблемам. Очевидно, что первый go to - это простой цикл, и приходим к тому, что пример 6c - это два вложенных цикла. А именно (в синтаксисе Даля):
Пример 6e:
procedure treeprint(t); integer t; value t;
begin integer stack S; S := empty;
loop:
loop while t != 0:
S <= t;
t := L[t];
repeat;
while nonempty(S):
t <= S;
print(A[t]);
t := R[t];
repeat;
end.
Кроме того, существует довольно простой способ понять эту программу, представив подходящие “инварианты цикла”. В начале первого (внешнего) цикла предположим, что содержимое стека сверху вниз равно tn, ..., t1 для некоторого n >= 0, тогда оставшаяся задача процедуры состоит в том, чтобы выполнить:
treeprint(t);
print(A[tn]); treeprint(R[tn]);
...;
print(A[t1]); treeprint(R[t1]); (*)
Другими словами, назначение стека - записывать отложенные обязательства по печати A и правых поддеревьев определенных узлов. После понимания этой концепции смысл программы становится ясен, и мы даже можем увидеть, как мы могли бы написать её, не задумываясь о рекурсивной формулировке или операторе go to: внутренний цикл обеспечивает t = 0, а затем программа уменьшает стек, сохраняя (*) в качестве условия, которое должно быть выполнено, в ключевых точках внешнего цикла.
Внимательный программист может заметить неэффективность в этой программе: когда L[t] = 0, мы кладем t в стек и сразу же достаём. Если в бинарном дереве есть узлы, то в среднем около половины из них будут иметь L[t] = 0, поэтому мы можем захотеть избежать этих дополнительных вычислений. Это нелегко сделать с примером 6e без серьёзной работы над структурой, но легко модифицировать пример 6c (или 6d), локализовав источник неэффективности:
Пример 6f:
procedure treeprint(t); value t; integer t;
begin integer stack S; S := empty;
L1: loop while t != 0:
L3: if L[t] != 0
then S <= t; t := L[t]; go to L1;
L2: t <= S;
fi;
print(A[t]);
t := R[t];
repeat;
if nonempty(S) then go to L2 fi;
end.
Здесь видно, что возможно дальнейшее упрощение: go to L1 можно заменить на go to L3, поскольку известно, что t не ноль.
Эквивалентная программа без go to, аналогичная примеру 6e, принимает вид:
Пример 6g:
procedure treeprint(t); value t; integer t;
begin integer stack S; S := empty;
loop until finished:
if t != 0
then
loop while L[t] != 0:
S <= t;
t := L[t];
repeat;
else
if nonempty(S)
then t <= S;
else finished;
fi;
fi;
print(A[t]);
t := R[t];
repeat;
end.
Я вывел эту программу, разбирая инвариант цикла (*) из примера 6e, а не пытаясь убрать go to из примера 6f. Таким образом, я уверен, что эта программа хорошо структурирована, и значит мне не удалось найти пример удаления рекурсии, при котором go to были бы строго необходимы. Интересно, что наши преобразования, изначально предназначенные для повышения эффективности, привели нас к новым открытиям и к программам, которые всё ещё обладают достойной структурой. Тем не менее, мне кажется, что пример 6f легче понять, чем 6g, учитывая, что читателю сообщается, из какой рекурсивной программы он получен, и какие преобразования были использованы. Рекурсивная программа тривиально корректна, а преобразования требуют лишь рутинной проверки. В то время как для изобретения (*) требуется озарение.
Есть ли польза в устранении рекурсии? Очевидно, что в этом примере не будет большого выигрыша, если узким местом является сама процедура печати. Но давайте заменим print(A[t]) на
i := i+1; B[i] := A[t];
То есть предположим, что вместо печати дерева мы просто хотим сохранить его содержимое в некоторый другой массив B. Тогда мы можем ожидать улучшения производительности.
После внесения этого изменения я сравнил рекурсивный пример 6 с итеративным примером 6d на двух основных компиляторах ALGOL. Нормализовав результаты так, чтобы 6d использовал 1.0 времени на узел дерева, с подавленной проверкой границ, я обнаружил, что соответствующая рекурсивная версия занимает около 2.1 единиц времени на узел при использовании компилятора ALGOL W для 360/67. А на компиляторе SAIL для PDP-10 это соотношение составило 1.16. (Кстати, относительное время выполнения примера 6f составило 0.8 при использовании ALGOL W и 0.7 при использовании SAIL).
Устранение булевых флагов
Другим важным преобразованием программы, несколько менее известным, является удаление булевых флагов путём дублирования кода. Следующий пример взят из работы Дейкстры над алгоритмом Хоара Quicksort. Идея заключается в перестановке элементов массива A[m] ... A[n] таким образом, чтобы они были разделены на две части. Левая часть A[m] ... A[j-1], для некоторого подходящего j, будет содержать все элементы, меньшие некоторого значения v. Правая часть A[j+1] ... A[n] будет содержать все элементы больше v. А элемент A[j], лежащий между этими частями, будет равен v. Разбиение выполняется сканированием слева до нахождения элемента больше v, затем сканированием справа до нахождения элемента меньше v, затем снова сканированием слева, и так далее, перемещая выбивающиеся элементы на противоположную сторону, пока два сканирования не сойдутся. Булева переменная up используется, чтобы отличать левое сканирование от правого.
Пример 7:
i := m; j := n;
v := A[j]; up := true;
loop:
if up
then if A[i] > v
then A[j] := A[i]; up := false fi;
else if v > A[j]
then A[i] := A[j]; up := true fi;
fi;
if up then i := i+1 else j := j-1 fi;
while i < j repeat;
A[j] := v;
Изменения и проверки up здесь занимают довольно много времени. В общем случае мы можем избавиться от булевой переменной, сохранив ее текущее значение в адресе выполнения кода, то есть продублировав программу. Пусть в одной части текста будет true, а в другой false, с переходами между этими двумя частями в соответствующих местах. Таким образом, пример 7 становится:
Пример 7a:
i := m; j := n;
v := A[j];
loop: if A[i] > v
then A[j] := A[i]; go to upf fi;
upt: i := i+1;
while i < j repeat; go to common;
loop: if v > A[j]
then A[i] := A[j]; go to upt fi;
upf: j := j-1;
while i < j repeat;
common: A[j] := v;
Обратите внимание, что мы снова получили программу, в которой есть переходы в середину цикла, но мы можем понять её, поскольку знаем, что она образована из ранее понятной программы путем известного преобразования.
Конечно, эта программа запутаннее первой, и мы должны снова спросить себя, стоит ли выигрыш в скорости этих затрат. Если мы пишем процедуру сортировки, которая будет многократно переиспользована, нас интересует скорость. Среднее время работы Quicksort было проанализировано Хоаром в его работе 1962 года, и оказалось, что при сортировке N элеменов, тело цикла в примере 7 выполняется примерно 2N ln N раз, а выражение up := false выполняется примерно 1/3 N ln N раз. Все остальные части общей программы сортировки (здесь они не показаны) имеют время выполнения порядка N или меньше, поэтому при достаточно большом N скорость этого внутреннего цикла определяет скорость всего процесса сортировки. (Кстати, рекурсивная версия Quicksort будет работать примерно так же быстро, поскольку накладные расходы на рекурсию не являются частью внутреннего цикла. Но в этом случае устранение рекурсии имеет большое значение по другой причине: сокращение потребности во вспомогательном размере стека с порядка N до log N.)
Используя эти факты о времени выполнения внутреннего цикла, мы можем провести количественное сравнение примеров 7 и 7a. Как и в случае с примером 1, лучше всего провести два сравнения: одно с ассемблерным кодом, который приличный программист написал бы для этих примеров, а другое - с объектным кодом, созданным типичным компилятором, выполняющим только локальную оптимизацию. Программист на ассемблере будет хранить i, j, v и up в регистрах, а типичный компилятор не будет использовать для них регистры, за исключением случаев случайного совпадения. При этих предположениях асимптотическое время работы всей программы Quicksort составляет:
assembled compiled
Example 7 20.667N ln N 55.333N ln N
Example 7a 15.333N ln N 40N ln N
То есть, пример 7a экономит более 25% времени.
Я показал этот пример Дейкстре, предупредив его, что переход к циклам может стать для него страшным шоком. Я был чрезвычайно рад получить его ответ:
Ваша техника хранения значения up в программном адресе, конечно, абсолютно безопасна. Я не упал в обморок! Я ни в коем случае не “боюсь” программы, построенной таким образом, но я не могу считать её красивой: это действительно то же самое повторение кода с тем же самым завершающим условием, которое “перекрашивается” по ходу вычислений.
Далее он сказал, что с нетерпением ждет того дня, когда машины станут настолько быстрыми, что нам не придётся оптимизировать наши программы, но всё же
На данный момент я полностью согласен с вашим выводом: если производительность важна, применяйте “дисциплинированную оптимизацию” к хорошей программе, корректность которой достоверно установлена. Тогда ваши манипуляции над текстом программы перестают быть грязным хаком, они вполне безопасны и обоснованы.
Мне трудно выразить ту радость, которую мне доставило это письмо. Это было похоже на отпущение грехов, поскольку мне больше не нужно испытывать чувство вины за свои оптимизированные программы.
Корутины (сопрограммы)
Несколько человек, прочитавших первый вариант этой статьи, заметили, что пример 7a, возможно, легче понять как результат устранения связей между корутинами а не булевыми флагами. Рассмотрим следующую программу:
Пример 7b:
coroutine move i;
loop: if A[i] > v
then A[j] := A[i];
resume move j;
fi;
i := i+1;
while i < j repeat;
coroutine move j;
loop: if v > A[j]
then A[i] := A[j];
resume move i;
fi;
j := j-1;
while i < j repeat;
i := m; j := n; v := A[j];
call move i;
A[j] := v;
Когда корутина “возобновляется”, будем считать, что она начинается после своего собственного оператора resume, а когда корутина завершается, будем считать, что тем самым завершается последний оператор вызова. (Фактическая связь между корутинами несколько сложнее, но для наших целей этого описания будет достаточно). В соответствии с этими соглашениями пример 7b в точности эквивалентен примеру 7a. В начале move i мы знаем, что A[k] < v для всех k < i, и что i < j, и что {A[m], ..., A[j-1], A[j+1], ..., A[n]} ∪ v является перестановкой исходного содержимого {A[m], . . ., A[n]}. Аналогичное утверждение справедливо и для начала move j. Такое разделение на две корутины делает пример 7b концептуально более простым, чем пример 7. Но, с другой стороны, к самому принципу работы корутин, конечно, нужно привыкнуть.
Кристофер Стрэчи однажды рассказал мне о примере, который впервые убедил его в том, что корутины обеспечивают важную структуру управления. Рассмотрим два двоичных дерева, представленных в примерах 5 и 6, с информацией из массива A в возрастающем порядке, поскольку мы обходим деревья в симметричном порядке их узлов. Задача состоит в том, чтобы объединить эти две последовательности массивов A в одну упорядоченную последовательность. Для этого нужно обойти оба дерева более или менее асинхронно, в симметричном порядке, поэтому нам понадобятся две версии примера 6, работающие совместно. Концептуально простое решение этой проблемы можно написать с помощью корутин или сформировать эквивалентную программу, которая выражает связь между корутинами с помощью операторов go to. Без использования одного из этих вариантов результат получится заметно более громоздким.
Quicksort: отступление
В своем письме Дейкстра привел ещё один поучительный пример. Он решил создать программу из примера 7 с нуля, как если бы алгоритм Хоара никогда не был изобретен, начав вместо этого с современных идей полуавтоматического построения программ, основанных на следующем инвариантном соотношении:
v = A[n] ∧
for all k(m <= k < i ⇒ A[k] <= v) ∧
for all k(j < k <= n ⇒ A[k] >= v).
Получившаяся программа необычна, но, пожалуй, чище, чем в примере 7:
i := m; j := n-1; v := A[n];
loop while i <= j;
if A[j] >= v then j := j-1;
else A[i] :=: A[j]; i := i+1;
fi;
repeat;
if j <= m then A[m] :=: A[n]; j := m fi;
Здесь “:=:” обозначает операцию обмена (т.е. swap). По завершении этой программы массив A будет не такой, как ранее, но мы получим его разбиение, необходимое для сортировки (т. е. A[m] ... A[j] <= v и A[j+1] ... A[n] >= v).
Однако, к сожалению, этот “чистый” код менее эффективен, чем пример 7, и Дейкстра отметил, что ему самому он не очень нравится. На практике Quicksort работает очень быстро, потому что существует метод, который даже лучше, чем пример 7a: быстрый внутренний цикл, который позволяет избежать большинства проверок i < j.
А недавно Дейкстра поделился со мной другим подходом к проблеме, который приводит к лучшему решению. Сначала мы можем рассмотреть общую ситуацию, определив понятия “малый (small)” и “большой (large)” так, чтобы:
- элемент
A[i]никогда не был одновременно и малым, и большим; - некоторые элементы могут быть и не малыми, и не большими;
- перестроенный массив получался таким, чтобы все малые элементы предшествовали всем большим;
- был хотя бы один элемент, который не является малым, и хотя бы один, который не является большим.
Тогда мы можем написать следующую программу в терминах этой абстракции:
Пример 8:
i := m; j := n;
loop:
loop while A[i] is small:
i := i+1; repeat;
loop while A[j] is large:
j := j-1; repeat;
while i < j:
A[i] :=: A[j];
i := i+1; j := j-1;
repeat;
В начале первого (внешнего) цикла мы знаем, что A[k] не “большое” для m <= k < i, и что A[k] не “малое” для j < k <= n, а также существует такое k, что i <= k <= n и A[k] не “малое”, и такое k, что m <= k <= j и A[k] не “большое”. Легко видеть, что операции в цикле сохраняют эти “инвариантные” условия. Заметим, что внутренние циклы теперь крайне быстры и гарантированно завершаются, поэтому доказать корректность работы просто. По завершении внешнего цикла мы знаем, что A[m] ... A[i-1] и A[j] не “большие”, что A[i] и A[j+1] ... A[n] не “малые”, и что m <= j <= i <= n.
Применив это к Quicksort, мы можем принять v := A[n] и записать
“A[i] < v” вместо “A[i] - малое“
“A[j] > v” вместо “A[j] - большое”
в приведённой выше программе. Это даёт очень красивый алгоритм, который по сути эквивалентен методу, опубликованному Хоаром в его первом крупном применении идеи инвариантов и рассмотренному в его оригинальной статье о Quicksort. Обратите внимание, что, поскольку v = A[n], мы знаем, что первое выполнение “loop while A[j] > v” будет тривиальным. Мы могли бы перенести этот цикл в конец внешнего цикла непосредственно перед финальным повтором. Это ещё добавит скорости, но сделает программу более сложной для понимания, поэтому я не решился это сделать.
Алгоритм разбиения Quicksort, приведенный в моей книге, лучше, чем пример 7a, но несколько отличается от программы, которую мы только что вывели. Моя версия может быть выражена следующим образом (при условии, что A[m-1] определено и не больше A[n]):
i := m-1; j := n; v := A[n];
loop until pointers have met:
loop: i := i+1; while A[i] < v repeat;
if i >= j then pointers have met; fi
A[j] := A[i];
loop: j := j-1; while A[j] > v repeat;
if i >= j then j := i; pointers have met; fi
A[i] := A[j];
repeat;
A[j] := v;
По завершении этой процедуры содержимое A[m] ... A[n] было изменено таким образом, что A[m] ... A[j-1] стали <= v, а A[j+1] ... A[n] => v и A[j] = v и m <= j <= n. Версия на ассемблере делает в среднем около 11N ln N обращений к памяти, так что эта программа на 28% быстрее примера 7a.
Когда я впервые увидел пример 8, то с досадой отметил, что его корректность проще доказать, чем мою программу. Он короче, и (сокрушительный удар) он примерно на 3% быстрее, потому что проверяет “i < j” вдвое реже. Мой первый математический анализ поведения примера 8 показал, что асимптотическое количество сравнений и обменов будет одинаковым, даже если разделенные подфайлы будут включать все N элементов, а не N-1, как в классической программе Quicksort. Но вдруг мне пришло в голову, что мой анализ неверен, потому что одно из его фундаментальных предположений рушится: элементы двух подфайлов после разбиения в примере 8 расположены не в случайном порядке! Это было неожиданностью, потому что случайность сохраняется в обычной процедуре Quicksort. Когда N ключей различны, v будет самым большим элементом в левом подмножестве, и механизм примера 8 показывает, что v будет стремиться оказаться слева от этого подмножества. При последующем разбиении этого подмножества велика вероятность, что v переместится в крайнюю правую часть полученного правого подмножества. Таким образом, это правое подмножество будет подвергнуто тривиальному разбиению по его наибольшему элементу и мы имеем незаметную потерю эффективности на третьем уровне рекурсии. Я пока ещё не проанализировал пример 8, но эмпирические тесты подтвердили мое предсказание, что он на самом деле примерно на 15% медленнее, чем мой книжный алгоритм.
Поэтому не стоит использовать пример 8 в реальных программах. Хотя он и выглядит немного чище, он заметно медленнее, так что не надо бояться использовать чуть более сложные методы, если они доказали свою корректность. Красивые алгоритмы, к сожалению, не всегда оказываются самыми полезными.
Но на этом история Quicksort не заканчивается (хотя мне бы очень хотелось, чтобы это было так). После того, как я показал пример 8 своему студенту Роберту Седжвику, он нашел способ модифицировать его, сохранив случайность в подмножествах, тем самым добившись одновременно элегантности и эффективности. Вот его переработанная программа:
Пример 8a:
i := m-1; j := n; v := A[n];
loop:
loop: i := i+1; while A[i] < v repeat;
loop: j := j-1; while A[j] > v repeat;
while i < j:
A[i] :=: A[j];
repeat;
A[i] :=: A[n];
Как и в предыдущем примере, мы предполагаем, что A[m-1] определено и не больше A[n], поскольку j может выйти за левую границу. В начале внешнего цикла инвариантные условия теперь таковы:
m-1 <= i < j <= n;
A[k] <= v for m-1 <= k <= i;
A[k] >= v for j <= k <= n;
A[n] = v.
Отсюда следует, что по завершении примера 8a A[m] ... A[i-1] <= v = A[i] <= A[i+1] ... A[n] и выполняется условие m <= i <= n, так что происходит реальное разделение.
Седжвик также нашел способ улучшить внутренний цикл алгоритма из моей книги:
i := m-1; j := n; v := A[n];
loop:
loop: i := i+1; while A[i] < v repeat;
A[j] := A[i];
loop: j := j-1; while A[j] > v repeat;
while i < j:
A[i] := A[j];
repeat;
if i != j then j := j+1;
A[j] := v;
Каждая из этих программ, применённая в Quicksort, в среднем даёт около 10,667N ln N обращений к памяти. Первый вариант предпочтительнее (за исключением машин, которые не поддерживают swap), поскольку его легче понять. Так что, я ещё раз убедился, что всегда нужно искать возможность улучшений, даже когда у вас уже есть хорошее решение.
Уменьшение сложности
Есть один вариант использования go to, для которого я так и не нашёл хорошей замены, и это тот случай, для которого я всё ещё считаю go to хорошим выбором. Этот случай возникает когда программа ветвится на большое число различных, но связанных между собой случаев и небольших изменений достаточно, чтобы свести два частных случая к одному общему. Когда мы свели задачу к более простой, наиболее естественным для нашей программы будет перейти к той процедуре, которая и решает более простую проблему.
Например, мы пишем интерпретатор программы или симулятор другого компьютера. После декодирования адреса и извлечения операнда из памяти мы выполняем ветвление на основе кода операции. Допустим, среди операций есть no-op, add, substract, jump on overflow и безусловный jump. Тогда процедура вычитания может выглядеть следующим образом:
operand := - operand; go to add;
процедура сложения может быть такой:
accum := accum + operand;
go to no op;
и команда перехода по переполнению:
if overflow
then overflow := false; go to jump;
else go to no op;
fi;
И я считаю, что это правильный способ написания такой программы.
Подобные ситуации не ограничиваются применением в интерпретаторах и симуляторах, хотя для них вышесказанное является особенно ярким примером. Множественное ветвление - важный прием программирования, который слишком часто заменяется неэффективной последовательностью if. Питер Наур недавно написал мне, что считает использование таблиц для управления потоком программ основной идеей информатики, которая была почти забыта, но он ожидает, что со дня на день она будет открыта вновь.
Некоторые намеки на ситуацию, когда одна задача сводится к другой, встречались в примерах этой статьи. Так, после поиска x и обнаружения его отсутствия, процедура not found может вставить x в таблицу, тем самым сведя задачу к случаю found. Возьмём наш пример 4 с таблицей принятия решений и предположим, что за каждой точкой должен следовать возврат каретки, а не дополнительный пробел. Тогда было бы естественно свести постобработку точек к части программы, связанной с возвратом каретки. И в каждом случае go to был бы понятен.
Если нам нужно найти способ обойтись без go to, мы можем расширить схему индикаторов событий Зана таким образом, чтобы некоторые события происходили в части then ... fi после того, как мы начали обрабатывать другие события. Это хорошо подходит для вышеупомянутых примеров, но может быть опасным, поскольку возвращает нам всю силу go to. Ограничение, позволяющее <statement list>i ссылаться на <event>j только при j > i, было бы менее опасным.
С такой особенностью языка мы не можем “вывалиться” из метки (то есть из индикатора события), когда достигнут конец предыдущего кода. Мы должны явно указывать имя события, когда переходим к его процедуре. Запрет на “проваливание” означает, что программист должен написать go to common непосредственно перед меткой common: в примере 7a. Удивительно, но такое изменение на самом деле делает программу более читабельной, а фрагмент программы
subtract: operand := - operand; go to add;
add: accum := accum + operand;
кажется чище, чем тот же самый, но без go to add. Интересно поразмышлять, почему так происходит.
3. Выводы
Это был долгий разговор, но можно выделить несколько моментов. Во-первых, есть несколько ситуаций в программировании, когда операторы go to не просто безвредны, но даже желательны, если мы программируем на ALGOL или PL/I. Во-вторых, разрабатываются новые типы синтаксиса, которые обеспечивают хорошую замену даже этим безвредным go to, не поощряя программиста создавать “логическое спагетти”.
Однако мы так и не смогли чётко сформулировать, что делает одни go to плохими, а другие - приемлемыми. Причина в том, что мы изучали не тот вопрос. Мы рассматривали проблему устранения go to, а не структуру программ. По словам Джона Брауна: “Сосредоточение наших мощнейших интеллектуальных ресурсов на труднодостижимой цели создания программ, не требующих go to, помогло нам отвлечься от всех тех действительно сложных и, возможно, неразрешимых проблем и вопросов, с которыми в противном случае пришлось бы столкнуться современному профессиональному программисту”.
Написав эту длинную статью, я не хочу подливать масла в огонь споров об устранении go to. Поскольку эта тема и так приобрела слишком большую значимость, моя цель - положить конец этим спорам и помочь направить дискуссию в более плодотворное русло.
Структурное программирование
Хотя мы и говорим о структурном программировании, к сожалению, этот термин начал жить своей жизнью и его смысл редко понимается одинаково разными людьми. Все знают, что это хорошая вещь, но, как сказал МакКракен: “Мало кто рискнёт дать определение. И даже не ясно, существует ли оно”. На самом деле понятно только то, что структурное программирование - это не процесс написания программ и последующего исключения из них операторов go to. В определении структурного программирования не должно вообще упоминаться про оператор go to. Тогда тот факт, что go to редко должны использоваться, будет простым следствием.
В оригинальной статье Дейкстры, давшей название структурному программированию, про go to нет ни слова. Он обратил внимание на критический вопрос: “Для каких структур программ мы можем без лишних усилий дать доказательства корректности, даже если программы будут большими?” Под доказательствами корректности он пояснил, что не имеет в виду формальные выводы из аксиом, а подразумевает любой вид доказательства (формального или неформального), которое является “достаточно убедительным”. И “доказательство” на самом деле означает “понимание”. Под структурой программы он подразумевает не только структуру данных, но и структуру управления.
Мы разбираемся со сложными вещами, разбивая их последовательно на более простые части и организуя их сочетания на локальном уровне. Таким образом, у нас есть разные уровни понимания, и каждый из этих уровней соответствует абстракции деталей на уровнях, из которых он состоит. Например, на одном уровне абстракции мы имеем дело с целым числом, не обращая внимания на то, представлено ли оно в двоичной системе счисления или в виде дополнительного кода и т. д., в то время как на более глубоких уровнях это представление может быть важным. На более абстрактных уровнях точное значение целого числа не имеет значения, за исключением того, как оно соотносится с другими данными.
Чарльз Л. Бейкер упомянул этот принцип еще в 1957 году в своей 8-страничной рецензии на первую книгу МакКракена по программированию: “Разбейте проблему на маленькие, самодостаточные подпрограммы, стараясь всё время изолировать разные участки кода, насколько это возможно… [тогда] проблема сводится к множеству гораздо более мелких. Опытным кодерам эта истина кажется совершенно очевидной, но новичкам её трудно объяснить.”
Абстракцию легко понять в терминах BNF-нотации. Такая металингвистическая категория, как <оператор присваивания>, - это абстракция, состоящая из двух других (<список слева> и <арифметическое выражение>), каждая из которых состоит из таких абстракций, как <идентификатор> или <выражение>, и т. д. Мы понимаем синтаксис программы в целом, зная структурные детали, которые связывают эти абстрактные части. Наиболее сложными для понимания в синтаксисе программы являются идентификаторы, поскольку их значение передается через несколько уровней структуры. Если все идентификаторы в программе на ALGOL заменить на случайные бессмысленные строки символов, нам было бы очень трудно понять, что делает программа, но мы бы легко распознали локальные вещи, такие как операторы присваивания, выражения, индексы и т. д. (Эта неспособность наших глаз связать тип или режим с идентификатором привела к фундаментальными ошибкам при разработке ALGOL 68, но это уже другая история. Моя собственная нотация для стека в примере 6c страдает от той же проблемы: она работает главным образом потому, что t - символ в нижнем регистре, а S - в верхнем). Большие вложенные структуры трудно разглядеть, если они не имеют отступов. Отступы делают структуру понятной.
Возможно, было бы ещё лучше, если бы мы изменили концепцию языков программирования так, чтобы программа не выглядела как одна длинная строка. Джон Маккарти сказал: “Мне трудно поверить, что всякий раз, когда я вижу дерево, я на самом деле вижу последовательность символов”.
Мы должны давать осмысленные имена крупным конструкциям в нашей программе, которые соответствуют осмысленным уровням абстракции, определить эти уровни абстракции в одном месте, и просто использовать их по именам, вместо того, чтобы включать их полный код, когда они используются для построения более крупных концепций. Именованные процедуры преследуют эту же цель, но язык можно легко спроектировать так, чтобы вызов подпрограммы не подразумевал никаких накладных расходов на это действие.
Из этих замечаний ясно, что последовательная композиция, цикл и условные выражения представляют собой синтаксические структуры, которые легко воспринимаются взглядом, а оператор go to - нет. Визуальная структура операторов go to похожа на структуру блок-схем, только в наших исходниках она сокращена до одного измерения. В двух измерениях можно воспринимать структуру go to в небольших примерах, но мы быстро теряем способность понимать более крупные блок-схемы. Необходимы некоторые промежуточные уровни абстракции.
Будучи студентом, в 1959 году я опубликовал блок-схему-осьминога, которая, как я искренне надеюсь, является самой ужасно сложной из всех, что когда-либо появлялись в печати. Всем, кто считает, что блок-схемы - лучший способ понять программу, настоятельно рекомендую взглянуть на неё  .
.
Я давно считаю, что талант программиста в значительной степени заключается в способности легко переключаться с микроскопического на макроскопический взгляд на вещи, то есть бегло менять уровни абстракции. Я упомянул об этом в адрес Дейкстры, и он прекрасно разобрал ситуацию:
Я чувствую себя несколько виноватым, за то, что предположил, что разграничение или введение “различных уровней абстракции” позволит вам думать только на одном уровне за раз, полностью игнорируя другие уровни. Это не так. Вы пытаетесь упорядочить свои мысли. То есть вы стремитесь расположить их таким образом, чтобы сконцентрироваться на какой-то части, скажем, на 90% вашего сознательного мышления, в то время как остальное временно отодвигается на задний план вашего разума. Но это совсем не “полное игнорирование”: вы позволяете себе временно не обращать внимание на детали, но некая общая оценка того, что должно быть, или должно появиться, всё ещё играет важную роль. Вы продолжаете следить боковым зрением за маленькими красными лампочками.
Синтаксическая структура - это только одна часть картины, и BNF была бы бесполезна, если бы синтаксические конструкции не соответствовали семантическим абстракциям. Аналогично, хорошая программа будет составлена таким образом, чтобы каждый семантический уровень абстракции имел достаточно простое отношение к своим составным частям.
Конструкция цикла должна иметь цель, которую достаточно легко сформулировать. Обычно эта цель состоит в том, чтобы сделать истинным определенное булево выражение, сохраняя при этом определенное инвариантное условие, которому удовлетворяют переменные. Булево условие указывается в программе, а инвариант должен быть указан в комментарии, если только он не очивиден для читателя. Например, в примере 1 инвариант состоит в том, что A[k] != x для 1 <= k < i, а в примере 2 - то же самое, плюс дополнительное A[m+1] = x. Оба эти условия настолько очевидны, что я не стал их упоминать, но в примерах 6e и 8 я указал более сложные инварианты. В каждом из этих случаев программа практически написалась сама собой, как только был задан соответствующий инвариант. Обратите внимание, что “определение инварианта” действительно немного меняется по мере выполнения операторов цикла, но к началу повторения цикла оно возвращается к своей первоначальной форме.
Таким образом, цикл является хорошей абстракцией, если мы можем назначить значимый инвариант, описывающий локальные состояния в процессе его выполнения, и если мы можем описать его цель (например, сменить одно состояние на другое). Аналогично, оператор if ... then ... else ... fi будет хорошей абстракцией, если мы можем указать общую цель для всего оператора.
Нам также нужны хорошо структурированные данные. То есть, когда мы пишем программу, мы должны иметь абстрактное представление о том, что означает каждая переменная. Это представление обычно можно описать в виде инвариантного отношения, например, “m - количество элементов в таблице” или “x - аргумент поиска” или “L[t] - номер корневого узла левого поддерева узла t, или 0, если это поддерево пусто” или “содержимое стека S - отложенные обязательства сделать то-то и то-то”.
Теперь рассмотрим немного более сложный случай событийно-ориентированной конструкции. Для каждого события мы приводим (инвариантное) утверждение, описывающее ситуацию, которая должна сложиться при наступлении этого события, а для loop until мы также приводим инвариант для цикла. Высказывание о событии обычно соответствует резкому изменению условий, так что необходимо утверждение, отличное от инварианта цикла.
Выход при ошибке можно считать хорошо структурированным именно по этой причине - он соответствует ситуации, которая невозможна, согласно утверждениям локального инварианта. Проще всего сформулировать утверждение, которое предполагает, что ошибок не будет, чем заставлять инварианты покрывать все непредвиденные ситуации. Когда мы выполняем переход при ошибке, мы переходим на другой уровень абстракции с другими предположениями.
В качестве другого простого примера рассмотрим двоичный поиск в упорядоченном массиве с использованием инвариантного отношения A[i] < x < A[j]:
loop while i+1 < j;
k := (i+j) / 2;
if A[k] < x then i := k;
else if A[k] > x then j := k;
else cannot preserve the invariant fi;
fi;
repeat;
При нормальном выходе из этого цикла условия i+1 >= j и A[i] < x < A[j] выражают, что A[i] < x < A[i+1], то есть что x не существует. Если программа переходит к cannot preserve the invariant (потому что x = A[k]), она хочет поменять набор предположений. Событийно-ориентированная конструкция обеспечивает уровень, на котором уместно такие предположения указать.
Ещё одна хорошая иллюстрация приведена в примере 6g: цель главного оператора if - найти первый узел, значение A которого должно быть выведено на печать. Если такого узла t не существует, то явно происходит событие finished. Поэтому лучше рассматривать оператор if как имеющий заявленную абстрактную цель, не принимая во внимание, что t может не существовать.
С операторами go to
С этой же точки зрения мы можем рассмотреть операторы go to: когда они соответствуют хорошей абстракции? Мы уже упоминали, что go to не имеют синтаксической структуры, которую глаз может уловить автоматически, но в этом отношении они ничем не хуже переменных и других идентификаторов. Когда им дается осмысленное имя, соответствующее абстракции, нам не нужно извиняться за отсутствие синтаксической структуры. А сама соответствующая абстракция является инвариантом, аналогичным проверкам, задаваемым для события.
Другими словами, мы действительно можем рассматривать операторы go to как часть систематической абстракции. Всё, что нам нужно - это чёткое представление о том, что именно означает переход go to для каждой метки. Это не должно удивлять. В конце концов, за последние 25 лет было написано множество компьютерных программ с использованием операторов go to, и далеко не все эти программы были неудачными! Некоторые программисты явно смогли овладеть структурой и использовать её. Возможно, не так строго, как в современном структурном программировании, но и совсем не расхлябанно. К настоящему времени многие люди, которые никогда не испытывали особых трудностей с написанием правильных программ, естественно, несколько расстроились после того, как их заклеймили грешниками, особенно, когда они прекрасно отдавали себе отчёт в том, что делали. Поэтому они, по понятным причинам, не испытывают особого энтузиазма по поводу рекламы и общего насаждения “структурного программирования”.
Я считаю, что, безусловно, можно писать хорошо структурированные программы и с операторами go to. Например, в программе Дейкстры 1965 года о параллельном управлении процессами использовались три оператора go to, и все они были совершенно просты для понимания, и я думаю, что максимум два из них исчезли бы из его кода, если бы в ALGOL 60 был оператор while.
Но сейчас go to вряд ли является лучшей альтернативой, поскольку в языках появляются более совершенные возможности. Если инвариант метки тесно связан с другим инвариантом, мы обычно можем сэкономить на сложности, объединив их в одну абстракцию, используя для этого не go to, а что-то другое.
Существует и другая проблема: на каком уровне абстракции появляется метка? С переменными есть похожая сложность, и в обоих случаях общий ответ пока не ясен. Аспекты структуры данных часто откладываются на потом, но иногда переменные определяются и передаются в качестве “параметров” на другие уровни абстракции. Похоже, что пока нет чёткого представления о наборе синтаксических соглашений, связанных с определением переменных, которые были бы наиболее подходящими для методологии структурного программирования, но для каждой конкретной проблемы, по-видимому, подходящий уровень существует.
Эффективность
В предыдущих рассуждениях мы пришли к выводу, что преждевременное акцентирование на эффективности - большая ошибка, которая вполне может быть источником большинства сложностей и проблем в программировании. Обычно при составлении программ соображения эффективности остаются на втором плане. Мы должны подсознательно помнить о доступных нам средствах обработки данных, но больше всего мы должны стремиться к тому, чтобы программа была легкой для понимания и почти наверняка заработала сразу. (Большинство программ, вероятно, нужны только один раз, и я полагаю, что в таких случаях нам не стоит слишком придираться даже к структуре, не говоря уже об эффективности).
Однако, когда эффективность программы важна, к счастью лишь очень небольшая часть кода обычно оказывает на неё существенное влияние. И когда мы готовы пожертвовать ясностью ради эффективности, можно создавать надежные программы, пригодные к поддержке в течение длительного времени, если начать с хорошо структурированной программы и затем использовать хорошо понятные преобразования, которые можно применять чисто механически. Мы не должны пытаться понять программу в её окончательном виде. Следует рассматривать её как результат исходной программы, изменённой с помощью некоторых преобразований.
В этой связи я хотел бы процитировать некоторые наблюдения, сделанные недавно Пьером-Арнулем де Марнеффом:
В гражданском проектировании в настоящее время обязательной концепцией, известной как “критерий проектирования Шенли”, является объединение нескольких функций в одну часть… Если вы сделаете поперечное сечение, например, немецкого V-2, вы найдете внешнюю обшивку, структурные стержни, стенки бака и т.д. Если же сделать поперечный разрез лунной ракеты “Сатурн-Б”, то можно обнаружить только внешнюю обшивку, которая одновременно является и структурным компонентом, и стенкой бака. Инженеры-ракетчики основательно применили “принцип Шенли”, когда использовали давление топлива внутри бака для повышения жесткости внешней обшивки! … Люди могут возразить, что структурные программы, даже если они работают правильно, будут выглядеть как лабораторные прототипы, в которых можно различить все отдельные компоненты, в то же время непригодные для повседневного использования. Создание “интегрированных” продуктов - это инженерный принцип, столь же ценный, как и структурирование процесса проектирования.
Далее он описывает планы по созданию прототипа системы, которая будет автоматически собирать интегрированные программы из хорошо структурированных компонентов, написанных сверху вниз путём пошагового уточнения.
Современные разработчики аппаратуры, безусловно, знают о преимуществах интегральных схем, но, конечно, они должны сначала научиться разбираться в компонентах, прежде чем приступать к интеграции. Ракета V-2 никогда бы не поднялась в воздух, если бы её конструкторы пытались сразу же объединить все функции. В инженерии есть две фазы, структурирование и интеграция: мы не должны забывать ни об одной из них, но лучше всего отложить фазу интеграции до тех пор, пока хорошо структурированный прототип не будет работать и при этом останется понятен. Как указал Вайнберг, прежний процесс анализа-кодирования-отладки должен быть заменён на анализ-кодирование-отладку-улучшение.
Будущее
Кажется очевидным, что языки, несколько отличающиеся от тех, что существуют сегодня, улучшат разработку структурных программ. Возможно, со временем мы будем писать только небольшие модули, давать им имена и строить из них более крупные, путём комбинирования, так что для выражения локальной структуры в исходном языке могут начать использоваться отступы, а не разделители.
Хотя наши примеры и не указывают на это, оказывается, что конкретный уровень абстракции часто включает несколько связанных процедур и определений данных. Например, когда мы решаем представить таблицу определенным образом, мы одновременно хотим указать процедуры для хранения и получения информации из этой таблицы. Следующее поколение языков, вероятно, будет учитывать такие связанные процедуры.
Системы преобразования программ представляются многообещающим инструментом будущего, который поможет программистам совершенствовать свои программы и получать от этого удовольствие. В настоящее время стандартной процедурой обычно является ручное кодирование критических частей программы на языке ассемблера. Будем надеяться, что необходимость в ассемблере уйдёт, и вместо него мы увидим несколько уровней языка: на самых высоких уровнях мы сможем писать абстрактные программы, а на самых низких - управлять хранением и распределением регистров, подавлять проверку индексов и т. д. В интегрированной системе можно будет проводить отладку и анализ преобразованной программы, используя для этого язык высокого уровня. Разумеется, на всех уровнях структура программы будет представлена синтаксически, чтобы её можно было читать и понимать.
Думаю, главный вопрос, хотя на самом деле он не должен быть таким уж большим, заключается в том, будут ли в конечном языке операторы go to на высших уровнях, или же go to будут ограничены низшими уровнями. Лично я не против иметь go to на высоком уровне, просто на случай, если он мне действительно понадобится, но я, вероятно, никогда не стал бы его использовать, если бы в языке присутствовали общие конструкции циклов и событий, предложенные в этой статье. Как только люди научатся осознанно применять принципы абстракции, они не будут видеть необходимости в go to, и проблема исчезнет сама. С другой стороны, Петерсон рассказал мне о своем опыте преподавания PL/I начинающим программистам: он учил их использовать go to только в необычных особых случаях, когда if и while не подходят, но он обнаружил, что “тревожно большой процент студентов сталкивался с ситуациями, требующими go to, потому, что while им не подходил из-за плохо продуманной реализации программы”. Из-за таких аргументов, как этот, я соглашусь, что нам действительно следует убрать go to из языков высокого уровня, хотя бы в качестве эксперимента по обучению людей более тщательному формулированию абстракций. Это действительно благотворно влияет на стиль, хотя я бы не стал вводить такой запрет, если бы в языке не было новых возможностей, описанных выше. Вопрос в том, что выбрать: запрет или обучение. Должны ли мы пытаться законодательно запретить go to? В такой постановке вопроса я голосую за закон, с доступными альтернативами взамен прежних неодолимых искушений.
Если мы действительно хотим иметь такой язык к 1984 году, необходимо провести большое количество исследований. Структура управления - это лишь одна небольшая проблема по сравнению с вопросами абстрактных структур данных. Удержать общее количество функций языка в жёстких рамках будет серьёзной проблемой. И мы должны обратить особое внимание на проблемы ввода/вывода и форматирования данных, чтобы обеспечить жизнеспособную альтернативу COBOL.
Благодарности
При подготовке этой работы мне была оказана поистине необычайная помощь. Эти люди предоставили мне в общей сложности 144 страницы комментариев, а также шесть часов бесед и четыре листинга программ:
Frances E. Allen, Ralph L. London, Forest Baskett, Zohar Manna, G. V. Bochmann, W. M. McKeeman, Per Brinch Hanse, Harlan D. Mills, R. M. Burstall, Peter Naur, Vinton Cerf, Kjell Overholt, T. E. Cheatham, Jr., James Peterson, John Cock, W. Wesley Peterson, Ole-Johan Dahl, Mark Rain, Peter J. Denning, John Reynolds, Edsger Dijkstra, Barry K. Rosen, James Eve, E. Satterthwaite, Jr., K. Friedenbach, D. V. Schorre, Donald I. Good, Jacob T. Schwartz, Ralph E. Gorin, Richard L. Sites, Leo Guiba, Richard Sweet, C. A. R. Hoare, Robert D. Tennent, Martin Hopkins, Niklaus Wirth, James J. Horning, M. Woodger, B. M. Leavenwort, William A. Wulf, Henry F. Ledgard, Charles T. Zahn.
Эти люди бескорыстно посвятили сотни человеко-часов, помогая мне переработать первый вариант статьи, и мне жаль, что я не смог примирить между собой все их интересные точки зрения. Во многих местах я беззастенчиво использовал их предложения без явного указания авторства. Эта статья - фактически совместный труд с 30-40 соавторами! Однако, все содержащиеся в ней ошибки - мои собственные.